Question
Question: The plane \(XOZ\) divides the join of \(\left( {1, - 1,5} \right){\text{ and }}\left( {2,3,4} \right...
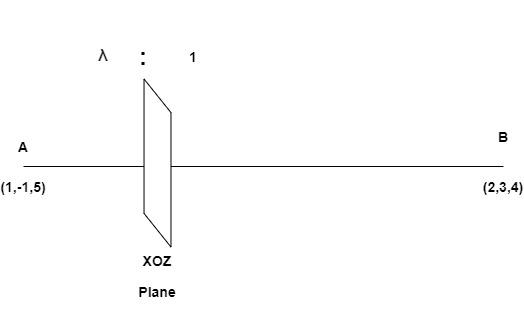
The plane XOZ divides the join of (1,−1,5) and (2,3,4) in the ratio λ:1, then λ is ?
A. - 3 B. 3−1 C. 3 D. 31
Solution
Hint: We will draw the figure and by using the figure we acknowledge the point where the plane cuts the line. Then, we will use section formula and find the value of λ and match that particular value with these options mentioned above.
Complete step-by-step answer:
Given points are (1,−1,5) and (2,3,4) and a planeXOZ where, X refers to x−plane, O refers to origin and Z refers to z−plane which cuts the line segment. Thus, the point is in XZ plane and cuts the line in a ratio of λ:1.
Using section formula i.e.
If the coordinates of the line (x1,y1,z1) and (x2,y2,z2) are divided in the ratio m:n then desired points will be (n+mnx1+mx2,n+mny1+my2,n+mnz1+mz2).
We can say, the desired points in our case will be (λ+12λ+1,λ+13λ−1,λ+14λ+5)
Since, this point then lies in XOZ plane then it’s y−coordinate should be zero.
∴ λ+13λ−1=0
We get
3λ−1=0 ⇒3λ=1 λ=31
Hence, the correct option is D. 31
Note: In the 3-D geometry we’ll use a section formula which tells us the coordinates of the points which divides a given line segment into two parts such that their lengths are in the ratio m:n. Do note that section formula is very helpful in coordinate geometry and in this question. Thus, this is the only way.
