Question
Question: The plane of a mirror makes an angle \( {30^ \circ } \) with the horizontal. If any vertical ray is ...
The plane of a mirror makes an angle 30∘ with the horizontal. If any vertical ray is incident on a mirror then the angle made by the reflected ray on the plane mirror will be.
Solution
Hint : To solve this question, construct the ray diagram for the reflection of the incident vertical ray on the mirror, then find the angle that this ray makes with the mirror by using the angle of the normal and angle of the mirror with the horizontal, then , by laws of reflection, the problem is solved.
The angle that the normal ray makes with the mirror is 90∘ .
The angle of incidence is equal to equal to the angle of reflection, i.e.
∠i=∠r
Complete Step By Step Answer:
Consider the plane mirror as given in the question that is making an angle of 30∘ with the horizontal, construct a vertical ray incident on the mirror and the corresponding reflected ray,
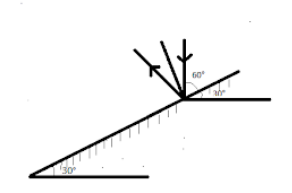
Here, the angle that the vertical incident ray makes with the mirror is:
90∘−30∘=60∘
Thus, the angle that the incident ray makes with the normal is
90∘−60∘=30∘
Now as according to the laws of reflection, the angle of incidence is equal to the angle of reflection, that means the angle that the reflected ray makes with the normal is equal to 30∘
Therefore, the angle that the reflected ray makes with the mirror surface is
90∘−30∘=60∘
Hence, the answer is 60∘ .
Note :
It is important to note that the incident vertical ray has to be perpendicular to the horizontal with which the angle of the mirror is already given, with this basic start, it gets very easier to solve this question, you might think of solving it the other way round by letting a variable for the value of angle that reflected ray makes with horizontal, but that makes it lengthy and tough.
