Question

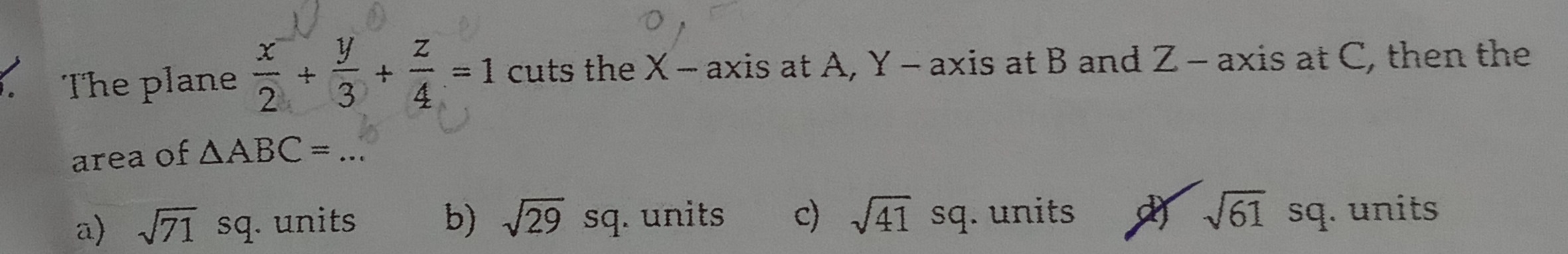
The plane $\frac{x}{2} + \frac{y}{3} + \frac{z}{4} = 1$ cuts the X-axis at A, Y-axis at B and Z-axis at C, then the area of $\triangle ABC = ...$

• A. $\sqrt{71}$ sq. units
• B. $\sqrt{29}$ sq. units
• C. $\sqrt{41}$ sq. units
• D. $\sqrt{61}$ sq. units

Answer 1

Answer: (D)

$\sqrt{61}$ sq. units

Answer 2

Solution:

The plane given is

$$\frac{x}{2} + \frac{y}{3} + \frac{z}{4} = 1.$$

Step 1: Find the intercepts on the axes.

• X-axis interception (A): Set $y=0, z=0$
  $\frac{x}{2}=1$ ⇒ $x=2$, so $A=(2,0,0)$.

• Y-axis interception (B): Set $x=0, z=0$
  $\frac{y}{3}=1$ ⇒ $y=3$, so $B=(0,3,0)$.

• Z-axis interception (C): Set $x=0, y=0$
  $\frac{z}{4}=1$ ⇒ $z=4$, so $C=(0,0,4)$.

Step 2: Calculate the area of $\triangle ABC$.

Let

$$\vec{AB} = B - A = (-2, 3, 0) \quad \text{and} \quad \vec{AC} = C - A = (-2, 0, 4).$$

Compute the cross product:

$$\vec{AB} \times \vec{AC} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ -2 & 3 & 0 \\ -2 & 0 & 4 \end{vmatrix} = \hat{i}(3 \cdot 4 - 0 \cdot 0) - \hat{j}((-2) \cdot 4 - 0 \cdot (-2)) + \hat{k}((-2) \cdot 0 - 3 \cdot (-2)).$$ $$=\hat{i}(12) - \hat{j}(-8) + \hat{k}(6) = (12, 8, 6).$$

The magnitude is:

$$\|\vec{AB} \times \vec{AC}\| = \sqrt{12^2 + 8^2 + 6^2} = \sqrt{144 + 64 + 36} = \sqrt{244} = 2\sqrt{61}.$$

Thus, the area of $\triangle ABC$ is:

$$\text{Area} = \frac{1}{2} \|\vec{AB} \times \vec{AC}\| = \frac{1}{2} \times 2\sqrt{61} = \sqrt{61}.$$