Question

The plane face of a Plano convex lens has been silvered. If $\mu$ be the refractive index and $R$, the radius of curvature of curved surface, then what is the radius of curvature if the system behaves like a concave mirror?
$\begin{aligned} & A.\mu R \\\ & B.\dfrac{{{R}^{2}}}{\mu } \\\ & C.\dfrac{R}{\left( \mu -1 \right)} \\\ & D.\left[ \dfrac{\left( \mu +1 \right)}{\left( \mu -1 \right)} \right]\times R \\\ \end{aligned}$

Answer 1

In this question, the light ray is getting refracted at so many places, as the plane surface of the Plano convex lens is silvered. Find out the effective focal length of the lens by taking care of all these refractions and the different surfaces. This focal length will be the same as that of a convex surface. These all details will help you to solve this question.

Complete step by step answer:

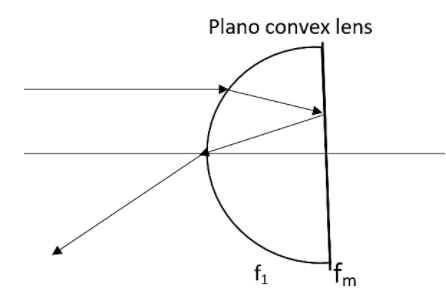
When an object is placed in front of such a Plano convex lens, the rays get reflected from the convex surface at first. After that the ray will refract from the polished plane surface and again gets refracted from the convex surface. Let us assume, ${{f}_{1}}$ ​and ${{f}_{m}}$ are the focal lengths of the lens. Where ${{f}_{1}}$ be the focal length of the convex surface and ${{f}_{m}}$ be the focal length of the plane polished surface which acts like a mirror.
Therefore the effective focal length of the lens is given by the equation,
$\dfrac{1}{F}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{m}}}$
As we already mentioned, the second surface is a plane surface. Therefore the radius of curvature of this surface will become infinity. And also it is understandable that the focal length is the half of the radius of curvature. Therefore we can write that,
$\begin{aligned} & {{R}_{m}}=\infty \\\ & {{f}_{m}}=\dfrac{{{R}_{m}}}{2}=\infty \\\ \end{aligned}$
So let us substitute the value of the focal length of the mirror into the effective focal length equation,
$\begin{aligned} & \dfrac{1}{F}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{\infty }+\dfrac{1}{{{f}_{1}}} \\\ & \dfrac{1}{F}=\dfrac{2}{{{f}_{1}}} \\\ \end{aligned}$
As we all know the focal length of lens is given by the equation,
$\dfrac{1}{{{f}_{1}}}=\mu -1\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]$
Substituting the given values in it,
$\dfrac{2}{{{f}_{1}}}=2\left( \mu -1 \right)\dfrac{1}{R}$
That is the focal length is,
${{f}_{1}}=F=\dfrac{R}{2\left( \mu -1 \right)}$
Therefore the radius of curvature will be,
$R=2F=\dfrac{R}{\left( \mu -1 \right)}$
Therefore the correct answer is given as option C.

Note:
The focal length of an optical equipment is defined as the amount of how powerfully the system can converge or diverge light rays. It is the reciprocal of the optical power of the system. A positive focal length is denoting that the system is converging light. The negative focal length is the result of divergence of light.