Question

The plane $ax + by + cz = 1$ containing the line $\frac{x-3}{2} = \frac{y-1}{4} = \frac{z-2}{5}$ is rotated through an angle $\frac{\pi}{2}$ about this line to contain the point $(4, 3, 7)$. Value of $\left(2a + 3b + \frac{c}{8}\right)$ equals

Answer 1

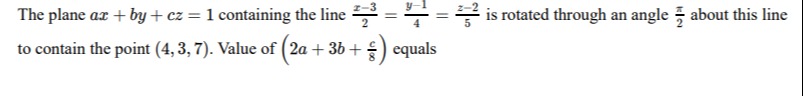
31/4

Answer 2

The problem involves a plane containing a line and then being rotated about that line. This implies the line is the intersection of the initial plane and the rotated plane.

1. Represent the line as the intersection of two planes: The given line is $L: \frac{x-3}{2} = \frac{y-1}{4} = \frac{z-2}{5}$. We can express this line as the intersection of two planes. From $\frac{x-3}{2} = \frac{y-1}{4}$: $4(x-3) = 2(y-1) \implies 4x - 12 = 2y - 2 \implies 4x - 2y - 10 = 0 \implies 2x - y - 5 = 0$. Let this be $P_A$. From $\frac{y-1}{4} = \frac{z-2}{5}$: $5(y-1) = 4(z-2) \implies 5y - 5 = 4z - 8 \implies 5y - 4z + 3 = 0$. Let this be $P_B$.

2. Equation of any plane containing the line: Any plane passing through the line $L$ (which is the intersection of $P_A$ and $P_B$) can be written in the form $P_A + \lambda P_B = 0$. So, the equation of such a plane is $(2x - y - 5) + \lambda(5y - 4z + 3) = 0$. Rearranging the terms: $2x + (5\lambda - 1)y - 4\lambda z + (3\lambda - 5) = 0$.

3. Identify the initial plane ($P_1$) and the rotated plane ($P_2$): Let the initial plane be $P_1$. It is given as $ax + by + cz = 1$, and it contains the line $L$. So, $P_1$ is of the form $2x + (5\lambda - 1)y - 4\lambda z + (3\lambda - 5) = 0$ for some specific value of $\lambda$. The normal vector of $P_1$ is $\vec{n_1} = (2, 5\lambda - 1, -4\lambda)$.

   The plane $P_1$ is rotated about $L$ to become $P_2$. This means $P_2$ also contains the line $L$. So, $P_2$ is also of the form $2x + (5\mu - 1)y - 4\mu z + (3\mu - 5) = 0$ for some specific value of $\mu$. The normal vector of $P_2$ is $\vec{n_2} = (2, 5\mu - 1, -4\mu)$.

4. Use the angle of rotation: The plane is rotated through an angle $\frac{\pi}{2}$, which means $P_1$ and $P_2$ are perpendicular. Therefore, their normal vectors must be orthogonal: $\vec{n_1} \cdot \vec{n_2} = 0$. $2(2) + (5\lambda - 1)(5\mu - 1) + (-4\lambda)(-4\mu) = 0$ $4 + (25\lambda\mu - 5\lambda - 5\mu + 1) + 16\lambda\mu = 0$ $41\lambda\mu - 5\lambda - 5\mu + 5 = 0$ (Equation A)

5. Use the point on the rotated plane ($P_2$): The rotated plane $P_2$ contains the point $(4, 3, 7)$. Substitute this point into the equation of $P_2$: $2(4) + (5\mu - 1)(3) - 4\mu(7) + (3\mu - 5) = 0$ $8 + 15\mu - 3 - 28\mu + 3\mu - 5 = 0$ Combine constant terms: $8 - 3 - 5 = 0$. Combine $\mu$ terms: $15\mu - 28\mu + 3\mu = (15 + 3 - 28)\mu = (18 - 28)\mu = -10\mu$. So, $0 - 10\mu = 0 \implies \mu = 0$.

6. Find the value of $\lambda$ for $P_1$: Substitute $\mu = 0$ into Equation A: $41\lambda(0) - 5\lambda - 5(0) + 5 = 0$ $-5\lambda + 5 = 0 \implies 5\lambda = 5 \implies \lambda = 1$.

7. Determine the equation of the initial plane ($P_1$): With $\lambda = 1$, the equation of $P_1$ is: $2x + (5(1) - 1)y - 4(1)z + (3(1) - 5) = 0$ $2x + 4y - 4z - 2 = 0$ Dividing by 2: $x + 2y - 2z - 1 = 0$ This can be written as $x + 2y - 2z = 1$.

8. Identify $a, b, c$ and calculate the final expression: Comparing $x + 2y - 2z = 1$ with $ax + by + cz = 1$, we get: $a = 1$, $b = 2$, $c = -2$. Now, calculate the value of $\left(2a + 3b + \frac{c}{8}\right)$: $2(1) + 3(2) + \frac{-2}{8}$ $= 2 + 6 - \frac{1}{4}$ $= 8 - \frac{1}{4}$ $= \frac{32 - 1}{4} = \frac{31}{4}$.

The final answer is $\boxed{\frac{31}{4}}$.