Question
Question: The pipe shows the volume flow rate of an ideal liquid at a certain time and its direction. What is ...
The pipe shows the volume flow rate of an ideal liquid at a certain time and its direction. What is the value of Q in sm3 ? ( Assume steady state and equal area of cross- section at each point).
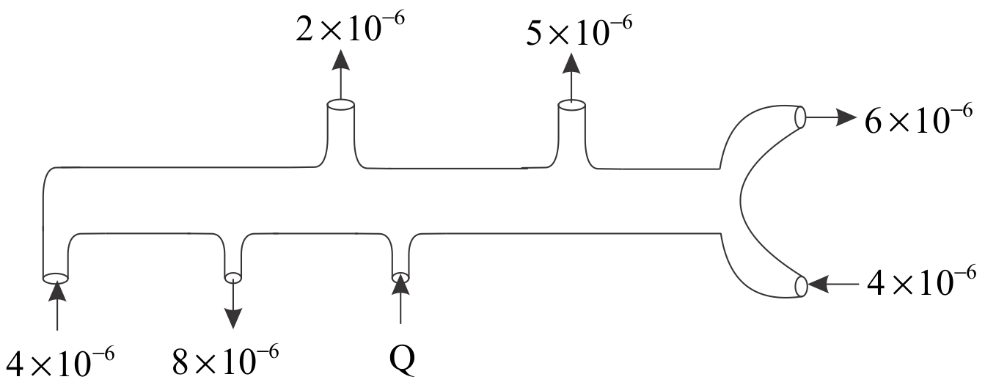
(A) 10×10−6
(B) 11×10−6
(C) 13×10−6
(D) 18×10−6
Solution
Apply the equation of continuity at all sections . The volume flowing inside the pipe will be equal to the volume flowing outside the pipe . All other values ( at each opening ) are given and this is how it can be calculated .
Complete step by step solution: The above problem will be solved by applying a continuity equation. The equation of continuity is based on conservation of mass . It states that the volume entering the pipe will be equal to the volume exiting the pipe ( if there aren’t any frictional losses) .
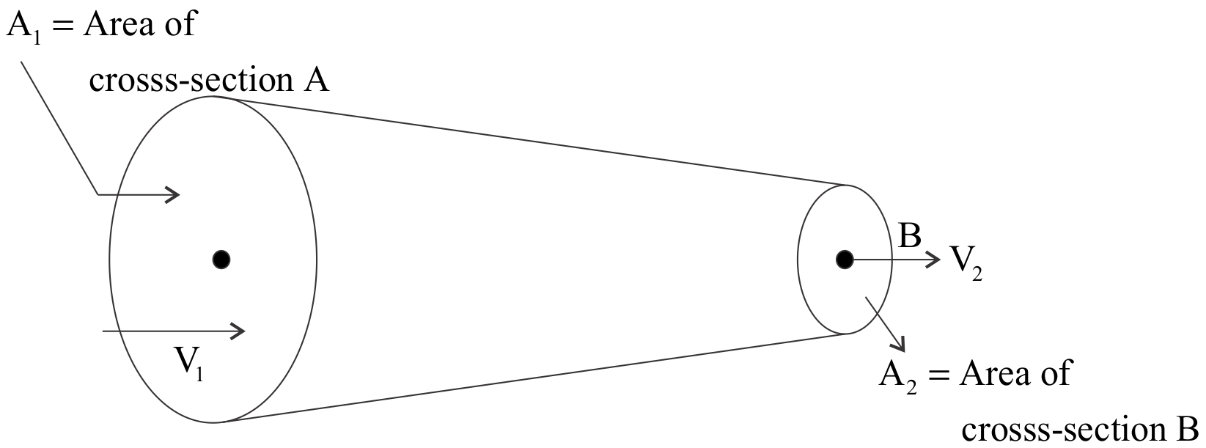
Suppose we have two sections A and B as shown in the diagram .
V1,V2 are the velocities of each section A and B respectively .
A1,A2 are the corresponding areas of cross- sections .
So according to equation of continuity:
A1V1=A2V2 ……..(i)
The flow rate of liquid is expressed in terms of area and velocity. So eq(i) can be written as :
Q1=Q2
In the above question, flow rate through each cross- section is given .
Flow rate incoming= flow rate outgoing
We have:
Qin=Qout (4×10−6)+(4×10−6)+Q=(2×10−6)+(5×10−6)+(8×10−6)+(6×10−6) Q=13×10−6
We have got the answer . The correct option is C.
Note: We need to keep in mind that in this derivation we have neglected the loss due to friction . If friction were to be present there will be slight loss in the volume of the liquid .
