Question

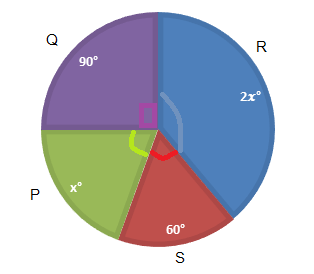
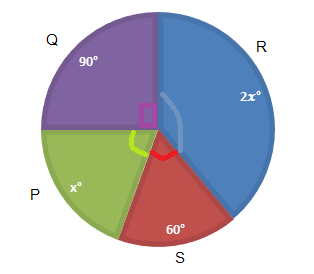
The pie chart shows the number of participants from four countries P, Q, R and S taking part in a tennis tournament. Given that there are $18$ participants from country S, find the number of participants from country R.

A. $18$
B. $21$
C. $27$
D. $42$

Answer 1

We have given a pie chart and it shows the number of participants from four countries taking part in a tennis tournament. Then we were given that there is some number of participants from one particular country and we asked to find the number of participants from another particular country.

Formula used: Area covered by a country $= \dfrac{{\theta \times {r^2}}}{2}$

Complete step-by-step solution:
Here it is given that,

From the circle diagram,
Sum of all angles of circle $= {360^\circ }$
$\Rightarrow {90^\circ } + 2{x^\circ } + {x^\circ } + {60^\circ } = {360^\circ }$
Add the coefficient of ${x^\circ }$
$\Rightarrow {90^\circ } + 3{x^\circ } + {60^\circ } = {360^\circ }$
Keep the ${x^\circ }$ terms in the left right side, we get
$3{x^\circ } = {360^\circ } - {150^\circ }$
$\Rightarrow 3{x^\circ } = {210^\circ }$
$\Rightarrow {x^\circ } = \dfrac{{{{210}^\circ }}}{{{3^\circ }}}$
$\Rightarrow {x^\circ } = {70^\circ }$
Given number of participants from country $S = {60^\circ }$
Number of participants from $S =$ Area covered by $S$
We have given that there are $18$ participants from $S$.
$\Rightarrow 18 = \dfrac{{\theta \times {r^2}}}{2}$
$\Rightarrow \dfrac{{\dfrac{\pi }{3} \times {r^2}}}{2} = 18$
Just keep ${r^2}$ on the left hand side and take all the remaining terms into the right hand side.
$\Rightarrow {r^2} = \dfrac{{18 \times 2 \times 3}}{\pi }$
$\Rightarrow {r^2} = \dfrac{{18 \times 6}}{\pi }$
$\therefore$ Number of participants from country $R = \dfrac{{\theta \times {r^2}}}{2}$
In the given pie chart, angle for the area covered by $R$ is $2{x^\circ }$.
$\therefore \theta = 2{x^\circ } = 2 \times {70^\circ } = {140^\circ }$
$\therefore$Number of participants from country $R = \dfrac{{\dfrac{{7\pi }}{9} \times {r^2}}}{2}$
$\Rightarrow \dfrac{{7\pi }}{{9 \times 2}} \times {r^2}$
$\Rightarrow \dfrac{{7\pi }}{{9 \times 2}} \times \dfrac{{18 \times 6}}{\pi }$
Simplifying the above equation, we get

$\therefore$ Number of participants from country $R = 42$

Note: In a circle the sum of the central angle of the minor and major segment is equal to $360$ degree. So we add up all the angles of the area covered by the given four participating countries and we equal the value to $360$ degree. If we have found our post searching for $\dfrac{{7\pi }}{9}$ radians to degrees, or a similar term, then we have gotten our answer as well $\dfrac{{7\pi }}{9} \Leftrightarrow {140^\circ }$.