Question

The picture shown below represents a planet (blue) orbiting a star. This particular planet has a highly elliptical orbit, as shown. At what point in the orbit is the planet moving the fastest?

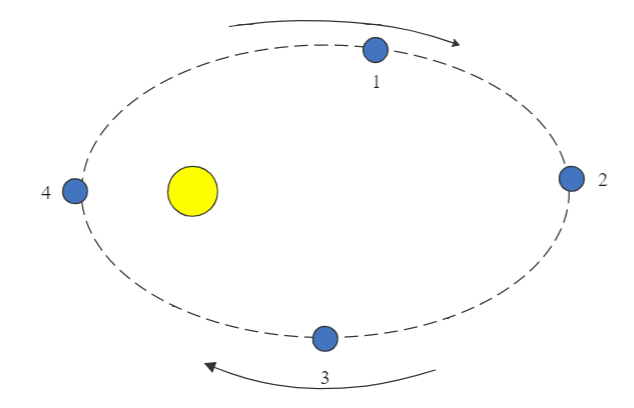
A. 1
B. 2
C. 3
D. 4
E. We cannot determine where the planet is moving the fastest, since Kepler’s Laws apply only to planets in our solar system.

Answer 1

Hint
Planetary motion is explained by Kepler’s laws of planetary motion. For a planet orbiting a star in an isolated system, the same rules apply as would in our solar system
Formula used: $L = mvr$ where $L$ is the angular momentum of the planet, $m$ is the mass of the planet, $v$ is the planet’s speed, and $r$ is the distance of the planet from its orbit to the star.

Complete step by step answer
We are provided with a single planet system around a star. We know that the angular momentum of a planet is given as:
$L = mvr$
According to the question, as the planet is moving in an elliptical orbit its angular momentum will remain constant. So will the mass. Bringing the constant terms $L$ and $m$ together on one side:
$\Rightarrow \dfrac{L}{m} = vr = {\text{ constant}}$
As the product of velocity and the distance to the star are constant, they exhibit an inverse relationship with each other.
This means as the radius decreases, the velocity will increase. So, to answer our question, the maximum velocity will occur when the distance is the smallest, and this happens at point 4.
Hence, the correct answer is option (D).

Note
We know that any two massive objects exert a force of gravity on each other. Since, the star weighs much more than the planet, the planet is bound to be attracted to the star. This causes the origin of orbits and the revolution of planets around stars. The Earth is at a distance of 149 million km from the Sun, but still orbits the Sun following precise physics. This is how further the range of gravitational attraction goes.