Question

The perpendicular bisector of the line segment joining the points $7 + 7i$ and $7 - 7i$ in the Argand diagram has the equation:
A.$y = 0$
B.$x = 0$
C.$y = x$
D.$x + y = 0$

Answer 1

Here, we will first draw the diagram and then by symmetry of the points with respect to the $x$-axis, we can say $x$–axis is the perpendicular bisector of the line segment joining $7 + 7i$ and $7 - 7i$ to find the required equation.

Complete step-by-step answer:
We are given that the perpendicular bisector of the line segment joining the points $7 + 7i$ and $7 - 7i$ in the Argand diagram has the equation.

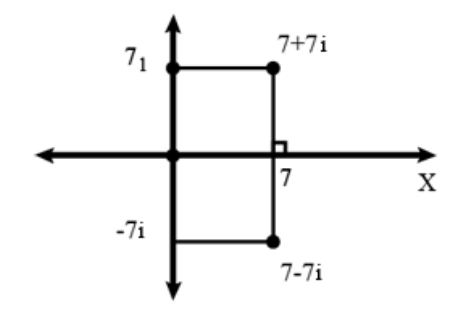
We know that the real part of the complex number has the $x$–value and the imaginary part of the complex number has the $y$–value.
Since we know that by symmetry of the points with respect to the $x$-axis, we can say $x$–axis is the perpendicular bisector of the line segment joining $7 + 7i$ and $7 - 7i$.
Thus, the required equation is $y = 0$.
Hence, option A is correct.

Note: In solving these types of questions, students must know about the real and imaginary parts of a complex number. One should know the symmetry of the points with the axis to find the equation, which is the perpendicular bisector of the line segment.