Question

The period of the function $f\left( x \right)=\dfrac{\left| \left. \sin \left( x \right) \right|-\left| \left. \cos \left( x \right) \right| \right. \right.}{\left| \left. \sin \left( x \right)+\cos \left( x \right) \right| \right.}$ is
(a) $\dfrac{\pi }{2}$
(b) $2\pi$
(c) $\pi$
(d) None of the above

Answer 1

Hint: We will apply the formula for finding the period of any trigonometric functions. The formula for this is given by f(x + q) = f(x) where q is called the period of the trigonometric function.

Complete step-by-step solution -
The required diagram for the function $f\left( x \right)=\dfrac{\left| \left. \sin \left( x \right) \right|-\left| \left. \cos \left( x \right) \right| \right. \right.}{\left| \left. \sin \left( x \right)+\cos \left( x \right) \right| \right.}$ is shown below.

Now, we will apply here the formula for finding period for the given function. First we need to understand that what does the term period means. The period of a trigonometric function is basically a cycle after which the repetition starts for the same function. For example we consider the sine function. The graph for the function is shown below.

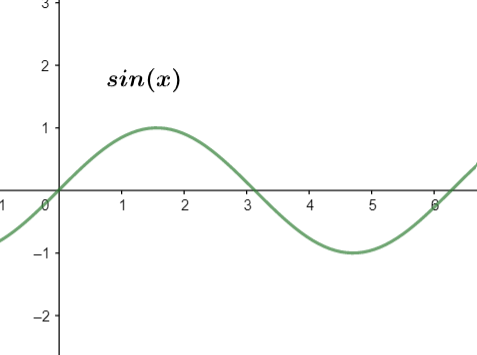
Clearly we can see that the waves that are produced by this function are at the regular intervals. Here we have that the function $\sin \left( x \right)$ has a period of $\pi$. This is because the waves are reappearing in the graph after every $\pi$ value.
Now, we will find the period for the function $f\left( x \right)=\dfrac{\left| \left. \sin \left( x \right) \right|-\left| \left. \cos \left( x \right) \right| \right. \right.}{\left| \left. \sin \left( x \right)+\cos \left( x \right) \right| \right.}$. We will apply the formula which is used for period. This is given by f(x + q) = f(x) where q is called the period of the trigonometric function. So, here we will start with the smallest positive q, and that is $\pi$. Now, we will substitute the value of q into the function. Therefore, we have
$\begin{aligned} & f\left( x \right)=\dfrac{\left| \left. \sin \left( x \right) \right|-\left| \left. \cos \left( x \right) \right| \right. \right.}{\left| \left. \sin \left( x \right)+\cos \left( x \right) \right| \right.} \\\ & \Rightarrow f\left( x+q \right)=\dfrac{\left| \left. \sin \left( x+\pi \right) \right|-\left| \left. \cos \left( x+\pi \right) \right| \right. \right.}{\left| \left. \sin \left( x+\pi \right)+\cos \left( x+\pi \right) \right| \right.} \\\ \end{aligned}$
As we know that the value of $\sin \left( x+\pi \right)=-\sin \left( x \right)$ and the value of $\cos \left( x+\pi \right)=-\cos \left( x \right)$ so, by these substitutions we have,
$\begin{aligned} & f\left( x+q \right)=\dfrac{\left| \left. \sin \left( x+\pi \right) \right|-\left| \left. \cos \left( x+\pi \right) \right| \right. \right.}{\left| \left. \sin \left( x+\pi \right)+\cos \left( x+\pi \right) \right| \right.} \\\ & \Rightarrow f\left( x+q \right)=\dfrac{\left| \left. -\cos \left( x \right) \right|-\left| \left. -\sin \left( x \right) \right| \right. \right.}{\left| \left. \cos \left( x \right)+\sin \left( x \right) \right| \right.} \\\ \end{aligned}$
Clearly, we have that f(x + q) = f(x). Thus, the smallest positive period of the function $f\left( x \right)=\dfrac{\left| \left. \sin \left( x \right) \right|-\left| \left. \cos \left( x \right) \right| \right. \right.}{\left| \left. \sin \left( x \right)+\cos \left( x \right) \right| \right.}$ is $\pi$.
Hence the correct option is (c).

Note: We could have also used here the angle q as $2\pi$ and it would also have resulted into f(x + q) = f(x). But we are supposed to find out the smallest positive period of the function. Therefore, we have chosen here $\pi$ instead of $2\pi$. Alternate method of finding the period of the function is by understanding it from the graph. Clearly, we can see from the graph that the function is repeating after every $\pi$ interval so we directly have that the period of the given function is $\pi$.