Question

The period of $f(x) = x-[x]$, if it is periodic, is

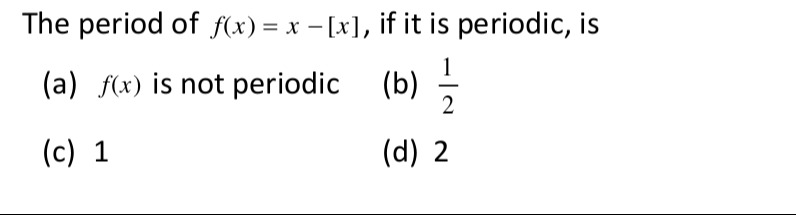
• A. $f(x)$ is not periodic
• B. $\frac{1}{2}$
• C. 1
• D. 2

Answer 1

Answer: (C)

1

Answer 2

The function is given by $f(x) = x - [x]$. This function represents the fractional part of $x$, denoted as $\{x\}$. Therefore, $f(x) = \{x\}$.

A function $f(x)$ is periodic with period $T > 0$ if $f(x+T) = f(x)$ for all $x$ in the domain of $f$. The smallest such positive value of $T$ is called the fundamental period.

We need to check if there exists a $T > 0$ such that $f(x+T) = f(x)$ for all $x$. This means we need to find a $T$ such that $(x+T) - [x+T] = x - [x]$ for all $x$.

Testing $T=1$:

$[x+1] - [x]$. Using the property of the greatest integer function, $[y+n] = [y] + n$ for any integer $n$, we have $[x+1] = [x] + 1$. Therefore, $[x+1] - [x] = ([x]+1) - [x] = 1$.

Thus, for $T=1$, the condition $T = [x+T] - [x]$ becomes $1 = [x+1] - [x]$, which is true for all $x$. This means $f(x+1) = (x+1) - [x+1] = (x+1) - ([x]+1) = x - [x] = f(x)$. So, $f(x)$ is periodic with period 1.

To confirm that 1 is the fundamental period, we must ensure there is no period $T_0$ such that $0 < T_0 < 1$.

Assume there exists a period $T_0 \in (0, 1)$. Then we must have $T_0 = [x+T_0] - [x]$ for all $x$.

Let's choose a specific value of $x$. Let $x=0$. Then $T_0 = [0+T_0] - [0] = [T_0] - 0 = [T_0]$. Since $0 < T_0 < 1$, $[T_0] = 0$. So, this requires $T_0 = 0$. But we are looking for a positive period, $T_0 > 0$. This is a contradiction.

Therefore, the fundamental period is 1.