Question
Question: The perimeter of the locus of the point at which the two circles $x^2 + y^2 = 1$ and $(x - 4)^2 + y^...
The perimeter of the locus of the point at which the two circles x2+y2=1 and (x−4)2+y2=4 subtend equal angles is
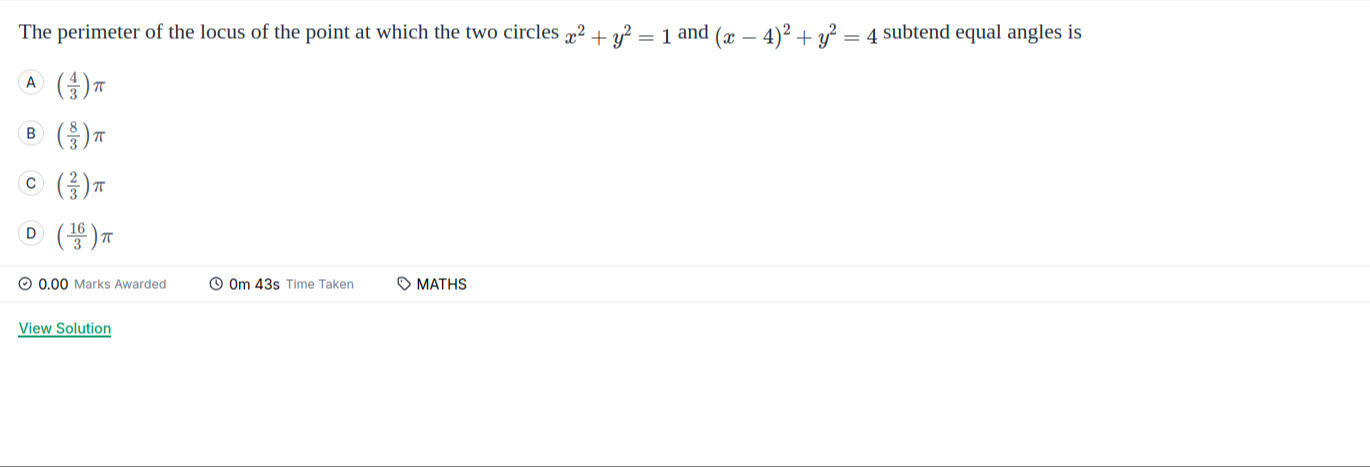
(34)π
(38)π
(32)π
(316)π
(316)π
Solution
Let the two circles be C1:x2+y2=1 with center O1=(0,0) and radius r1=1, and C2:(x−4)2+y2=4 with center O2=(4,0) and radius r2=2.
Let P(x,y) be a point on the locus. The angle subtended by a circle of radius r at an external point P at a distance d from the center is 2α, where sinα=dr.
For C1, the distance from P(x,y) to O1(0,0) is d1=x2+y2. The angle subtended is 2α1, where sinα1=d1r1=x2+y21. For C2, the distance from P(x,y) to O2(4,0) is d2=(x−4)2+y2. The angle subtended is 2α2, where sinα2=d2r2=(x−4)2+y22.
The condition that the two circles subtend equal angles at P implies 2α1=2α2, so α1=α2. Since P must be external to both circles for the angles to be defined as above, d1>r1 and d2>r2, which means 0<sinα1<1 and 0<sinα2<1. Thus, α1 and α2 are acute angles.
Equating the sines: sinα1=sinα2 d11=d22 x2+y21=(x−4)2+y22 Squaring both sides: x2+y21=(x−4)2+y24 (x−4)2+y2=4(x2+y2) Expanding and rearranging: x2−8x+16+y2=4x2+4y2 3x2+3y2+8x−16=0 Dividing by 3: x2+y2+38x−316=0 Completing the square for the x terms: (x2+38x)+y2=316 (x+34)2−(34)2+y2=316 (x+34)2+y2=316+916 (x+34)2+y2=948+16 (x+34)2+y2=964 This is the equation of a circle with center C=(−34,0) and radius R=964=38.
The perimeter of this locus circle is 2πR. Perimeter =2π(38)=316π.
The analysis in the raw solution confirms that all points on this locus are indeed external to both original circles, validating the method used.
