Question

The perimeter of a sector is a constant. If its area is to be maximum , then the sectorial angle is
A. $\dfrac{{{\pi }^{c}}}{6}$
B. $\dfrac{{{\pi }^{c}}}{4}$
C. ${{4}^{c}}$
D. ${{2}^{c}}$

Answer 1

To solve the above question first we will know the definition of sector or circle sector. A circle sector is the portion of a disk which is enclosed by two radii and an arc.

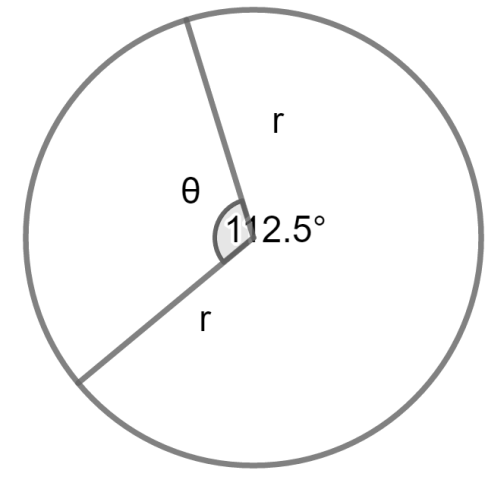
In the diagram, $\theta$ is the central angle, r is the radius of the circle. If $\theta$is measured in radians, then, area of sector = $\dfrac{1}{2}{{r}^{2}}\theta$ and the perimeter of the sector is $2r+r\theta$

Complete step by step solution:
Let r be the radius of the circle and $\theta$ be the sectorial angle of a sector of it. Then the perimeter of the sector is :
$\Rightarrow 2r+r\theta =k$
Where, k is the constant which is given in the question.
By above equation we will find the radius of the circle as:
$\Rightarrow r=\dfrac{k}{2+\theta }..........\left( 1 \right)$
Let A be the area of the sector, then we get
$\Rightarrow A=\dfrac{1}{2}{{r}^{2}}\theta$
Now put the value of r from equation (1) in the above equation, we get
$\Rightarrow A=\dfrac{1}{2}\cdot \dfrac{{{k}^{2}}}{{{\left( 2+\theta \right)}^{2}}}\cdot \theta$
Now on differentiating on both sides with respect to $\theta$, we get
\begin{aligned} & \Rightarrow \dfrac{dA}{d\theta }=\dfrac{{{k}^{2}}}{2}\left\\{ \dfrac{{{\left( \theta +2 \right)}^{2}}-2\theta \left( \theta +2 \right)}{{{\left( \theta +2 \right)}^{4}}} \right\\} \\\ & \Rightarrow \dfrac{dA}{d\theta }=\dfrac{{{k}^{2}}}{2}\dfrac{\left( 2-\theta \right)}{{{\left( \theta +2 \right)}^{3}}} \\\ \end{aligned}
For maximum area, put $\dfrac{dA}{d\theta }=0$

& \Rightarrow 0=\dfrac{{{k}^{2}}}{2}\dfrac{\left( 2-\theta \right)}{{{\left( \theta +2 \right)}^{3}}} \\\ & \Rightarrow \theta =2 \\\ \end{aligned}$$ Now again differentiating $\dfrac{dA}{d\theta }=\dfrac{{{k}^{2}}}{2}\dfrac{\left( 2-\theta \right)}{{{\left( \theta +2 \right)}^{3}}}$, we get $\begin{aligned} & \Rightarrow \dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}=\dfrac{{{k}^{2}}}{2}\left[ \dfrac{2\times \left( -3 \right)}{{{\left( \theta -2 \right)}^{4}}}-\dfrac{{{\left( \theta +2 \right)}^{3}}\times 1-\theta \times 3{{\left( \theta +2 \right)}^{2}}}{{{\left[ {{\left( \theta +2 \right)}^{3}} \right]}^{2}}} \right] \\\ & \Rightarrow \dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}=\dfrac{{{k}^{2}}}{2}\left[ \dfrac{-6}{{{\left( \theta +2 \right)}^{4}}}-\dfrac{\theta +2-3\theta }{{{\left( \theta +2 \right)}^{4}}} \right] \\\ & \Rightarrow \dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}=\dfrac{-{{k}^{2}}}{2}\left[ \dfrac{6}{{{\left( \theta +2 \right)}^{4}}}+\dfrac{2-\theta }{\left| {{\left( \theta +2 \right)}^{4}} \right|} \right] \\\ \end{aligned}$ Now for maximum we already find out the value of $\theta =2$ , now put this value of $\theta $ in the above equation, we get $\begin{aligned} & \Rightarrow \dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}=\dfrac{-{{k}^{2}}}{2}\left[ \dfrac{6}{{{4}^{4}}}+0 \right] \\\ & \Rightarrow \dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}=\dfrac{-3{{k}^{2}}}{256} \\\ \end{aligned}$ Therefore the above value is greater than zero. Hence the area is maximum, when $\theta ={{2}^{c}}$. **So, the correct answer is “Option D”.** **Note:** We can go wrong in the calculation part. Here to differentiate the area we use the quotient rule of differentiation which is as: $\dfrac{d\left( \dfrac{u}{v} \right)}{dx}=\dfrac{u\grave{\ }v-v\grave{\ }u}{{{v}^{2}}}$ on both times . in $\theta ={{2}^{c}}$where c is the constant positive value.