Question

The perimeter of a quadrant of a circle of radius r is:
(a) $\dfrac{\pi r}{2}$
(b) $2\pi r$
(c) $\dfrac{r}{2}\left( \pi +4 \right)$
(d) $2\pi r+\dfrac{r}{2}$

Answer 1

Here, we will try to find the perimeter of the quadrant of a circle by using the formula for the perimeter of a circle which is $2\pi r$. We will the concept that a quadrant of a circle is one-fourth of a circle.

Complete step-by-step answer:

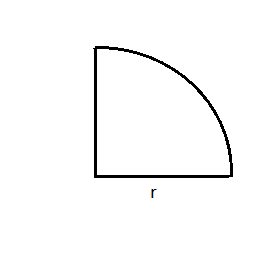
We know that a circle is defined as the locus of all the points that are equidistant from a fixed point called the centre of the circle. Now, a quadrant is one-fourth section of a circle which is obtained when a circle is divided evenly into four sections or rather 4 quadrants by a set of two lines which are perpendicular in nature.
Since, quadrant refers to the four quarters in the coordinate system. But, when it comes to a circle, the quarter of a circle is called a quadrant, which is a section of 90 degrees. When four such quadrants are joined, then we get a complete circle.
If the radius of a circle is r, then the perimeter of the circle is given as:
$P=2\pi r$
While finding the perimeter of a quadrant we need to add two times the radius of the circle to the perimeter of the curved boundary.
Perimeter of the curved boundary= $\dfrac{1}{4}\times 2\pi r$= $\dfrac{\pi r}{2}$
Now, on adding two times the radius of the circle to $\dfrac{\pi r}{2}$, we get:
$\begin{aligned} & 2r+\dfrac{\pi r}{2} \\\ & =\dfrac{r}{2}\left( \pi +4 \right) \\\ \end{aligned}$
Hence, option (c) is the correct answer.
Note: Students should note here that the quadrant of a circle is one-fourth section of the circle. So, for finding the perimeter of the quadrant, we have to take one-fourth of the circumference of the circle. One should also keep in mind that two times the radius of the circle have to be added to on-fourth the circumference of the circle.