Question

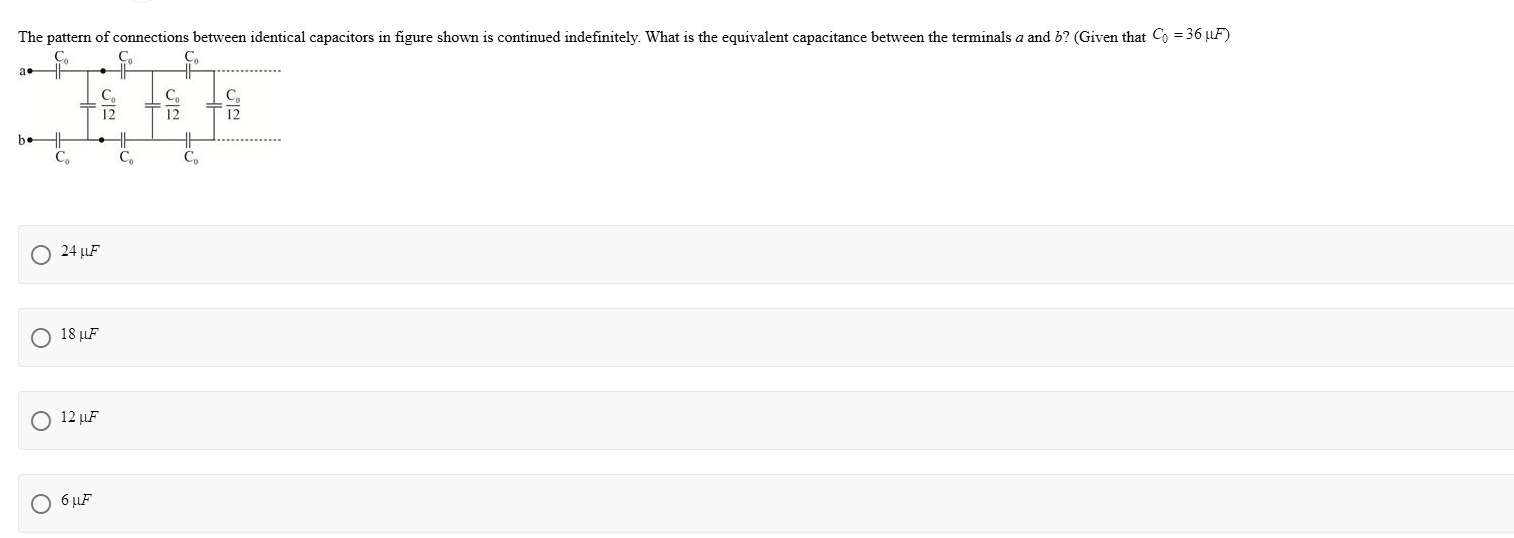
The pattern of connections between identical capacitors in figure shown is continued indefinitely. What is the equivalent capacitance between the terminals a and b? (Given that $C_0 = 36 \ \mu F$)

• A. 24 $\mu F$
• B. 18 $\mu F$
• C. 12 $\mu F$
• D. 6 $\mu F$

Answer 1

Answer: (D)

6 $\mu F$

Answer 2

The problem describes an infinite ladder network of capacitors. To find the equivalent capacitance of such a network, we use the property of self-similarity.

Let the equivalent capacitance between terminals 'a' and 'b' be $C_{eq}$. The network consists of a repeating unit. If we consider the first repeating unit and attach the rest of the infinite network to its output terminals, the equivalent capacitance of the remaining infinite network will also be $C_{eq}$.

Let's identify the first repeating unit and how the rest of the network connects. The first unit consists of:

1. A capacitor $C_0$ in the upper horizontal branch (connected from 'a' to an internal node, let's call it 'x').
2. A capacitor $C_0$ in the lower horizontal branch (connected from 'b' to an internal node, let's call it 'y').
3. A capacitor $C_0/12$ connecting the upper and lower internal nodes ('x' and 'y').

The remainder of the infinite network is connected between nodes 'x' and 'y'. Since the network is infinite and repeating, the equivalent capacitance of this remaining part is also $C_{eq}$.

So, the circuit can be redrawn as:

• A capacitor $C_0$ in series with the combination of capacitors between 'x' and 'y', on the top branch.
• A capacitor $C_0$ in series with the combination of capacitors between 'x' and 'y', on the bottom branch.
• The capacitance between 'x' and 'y' is formed by $C_0/12$ in parallel with $C_{eq}$ (the rest of the infinite network).

Let $C_{xy}$ be the equivalent capacitance between nodes 'x' and 'y'. Since $C_0/12$ and $C_{eq}$ are in parallel, their equivalent capacitance is: $C_{xy} = C_{0}/12 + C_{eq}$

Now, the total equivalent capacitance $C_{eq}$ between 'a' and 'b' is the series combination of the top $C_0$, the parallel combination $C_{xy}$, and the bottom $C_0$. For capacitors in series, the reciprocal of the equivalent capacitance is the sum of the reciprocals of individual capacitances: $\frac{1}{C_{eq}} = \frac{1}{C_0} + \frac{1}{C_{xy}} + \frac{1}{C_0}$

Substitute $C_{xy}$: $\frac{1}{C_{eq}} = \frac{1}{C_0} + \frac{1}{C_{0}/12 + C_{eq}} + \frac{1}{C_0}$ $\frac{1}{C_{eq}} = \frac{2}{C_0} + \frac{1}{C_{0}/12 + C_{eq}}$

To solve for $C_{eq}$, let $C_{eq} = x$: $\frac{1}{x} = \frac{2}{C_0} + \frac{1}{C_0/12 + x}$ Rearrange the equation: $\frac{1}{x} - \frac{2}{C_0} = \frac{1}{C_0/12 + x}$ $\frac{C_0 - 2x}{xC_0} = \frac{1}{C_0/12 + x}$ Cross-multiply: $(C_0 - 2x)(C_0/12 + x) = xC_0$ Expand the left side: $C_0^2/12 + C_0x - 2x(C_0/12) - 2x^2 = xC_0$ $C_0^2/12 + C_0x - xC_0/6 - 2x^2 = xC_0$ Subtract $xC_0$ from both sides: $C_0^2/12 - xC_0/6 - 2x^2 = 0$ Multiply the entire equation by 12 to eliminate fractions: $C_0^2 - 2xC_0 - 24x^2 = 0$ Rearrange into a standard quadratic equation form $ax^2 + bx + c = 0$: $24x^2 + 2C_0x - C_0^2 = 0$

Use the quadratic formula $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$: Here, $a = 24$, $b = 2C_0$, $c = -C_0^2$. $x = \frac{-2C_0 \pm \sqrt{(2C_0)^2 - 4(24)(-C_0^2)}}{2(24)}$ $x = \frac{-2C_0 \pm \sqrt{4C_0^2 + 96C_0^2}}{48}$ $x = \frac{-2C_0 \pm \sqrt{100C_0^2}}{48}$ $x = \frac{-2C_0 \pm 10C_0}{48}$

Since capacitance must be a positive value, we take the positive root: $x = \frac{-2C_0 + 10C_0}{48}$ $x = \frac{8C_0}{48}$ $x = \frac{C_0}{6}$

So, the equivalent capacitance $C_{eq} = \frac{C_0}{6}$. Given $C_0 = 36 \ \mu F$: $C_{eq} = \frac{36 \ \mu F}{6} = 6 \ \mu F$.

The equation $24C_{eq}^2 + 2C_0C_{eq} - C_0^2 = 0$ yields $C_{eq} = C_0/6$. Substituting $C_0 = 36 \ \mu F$, we get $C_{eq} = 36/6 = 6 \ \mu F$.