Question

The path of oscillation of a simple pendulum of length 1 meter is 16cm. Its maximum velocity is ($g={{\pi }^{2}}m/{{s}^{2}}$)

$A.2\pi cm/s$
$B.4\pi cm/s$
$C.8\pi cm/s$
$D.16\pi cm/s$

Answer 1

Hint:
Making a sample diagram of a simple pendulum executing SHM will help in understanding this question. The path of oscillation means the sum maximum displacements, excluding the direction.

Step by step solution:

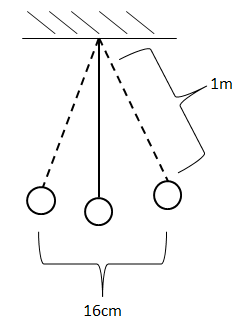
In this question, we don’t need to use all the formulas for the simple pendulum executing a SHM. We just need 2 basic ones.

The first one is about the time period of the oscillation for a simple pendulum $T=2\pi \sqrt{\dfrac{l}{g}}$, where $l$ stands for length of pendulum and $g$stands for acceleration due to gravity.

So, here using the given parameters, the time period of the oscillation will be,

$T=2\pi \sqrt{\dfrac{1}{{{\pi }^{2}}}}$

$T=\dfrac{2\pi }{\pi }$

Therefore we get $T=2s.$

Moving on the next part, as said above the second formula required to solve this question is related to the path of oscillation. This essentially means the sum of maximum displacements with respect to the center or the equilibrium position. For an ideal case, that’s here, we will consider both the displacements are equal. Hence the displacement $x=a\sin (\omega t)$for maximum displacement case will have$\sin (\omega t)=1$. Therefore $x=a$is the maximum displacement along one direction. Hence, $16cm=2a.$That makes the amplitude $a=8cm.$

Lastly to find the maximum velocity, we will use the formula $v=\omega a.$

$v=\dfrac{2\pi }{T}a$

Substituting in the found values here, $v=\dfrac{2\pi }{2s}8cm$

We get, $v=8\pi cm/s$

Note:
Remembering the formula for maximum velocity of a simple pendulum is necessary to easily get the solution.
For the path of oscillation, don’t consider the displacements with their directions, that’s the +ve and –ve sign. This will lead to both the displacements canceling each other.