Question

The path length of one oscillation of a simple pendulum of length of $1$ meter is $16cm$ . Its maximum velocity is ( $g = {\pi ^2}m{s^{ - 2}}$ )
\left( A \right)2\pi m{s^{ - 1}} \\\ \left( B \right)4\pi m{s^{ - 1}} \\\ \left( C \right)8\pi m{s^{ - 1}} \\\ \left( D \right)16\pi m{s^{ - 1}} \\\

Answer 1

Hint : In order to solve this question, we are going to draw a schematic diagram of the pendulum and then calculate the height $h$ of the pendulum bob from the length $AOB$ and then, by equating the potential and the kinetic energies of the pendulum bob, the maximum velocity is calculated.
The formula used in this question is
The angle $\theta = \dfrac{{arc}}{{radius}}$
All of the potential energy at $A$ is converted to the kinetic energy at $O$
P.E. = K.E. \\\ mg\Delta x = \dfrac{1}{2}m{v^2} \\\

Complete Step By Step Answer:
Let us first draw the figure for the given arrangement

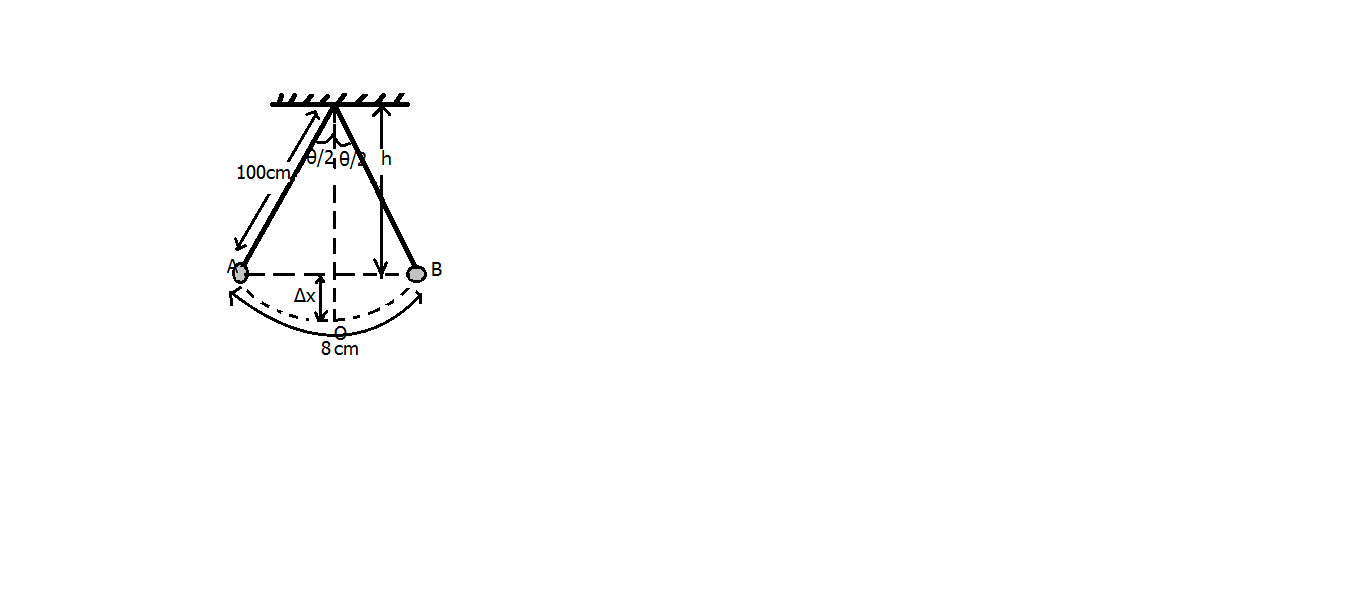
As it is given that the length of the complete oscillation is $16cm$ so, the length of $AOB$ will be $8cm$ , Now the angle $\theta = \dfrac{{arc}}{{radius}}$
Putting the values of the arc and the radius
$\theta = \dfrac{{8cm}}{{100cm}} = 0.08$
So, the angles $\dfrac{\theta }{2}$ equals $0.04$ radians
So, the height, $h$ is calculated as
h = 100cm \times \cos \dfrac{\theta }{2} = 100cm \times \cos \left( {0.04} \right) \\\ \Rightarrow h = 100cm \times 0.9992 = 99.92cm \\\
Therefore, $\Delta x = 100cm - h = 100 - 99.92 = 0.08cm$
Now, all of the potential energy at $A$ is converted to the kinetic energy at $O$
$P.E. = K.E.$
So,
$mg\Delta x = \dfrac{1}{2}m{v^2}$
Now, as it is given that, $g = {x^2} = \dfrac{1}{2}{v^2} = 100{\pi ^2}cm{s^{ - 2}}$
Since, $1m = 100cm$
Therefore,
g\Delta x = \dfrac{1}{2}{v^2} \\\ {v^2} = 2g\Delta x \\\ {v^2} = 2 \times 100{\pi ^2}cm{s^{ - 2}} \times 0.08cm \\\ {v^2} = 16{\pi ^2}c{m^2}{s^{ - 2}} \\\ v = 4\pi cm{s^{ - 1}} \\\

Note :
The angle $\theta$ is divided equally by the perpendicular bisector to the line segment. As the pendulum bob moves from a certain height to the reference level, all of its potential energy due to a particular height gets converted to the kinetic energy and when the bob goes from the reference level to the extreme point, the kinetic energy gets converted to the potential energy , this gives an energy equivalence.