Question

The parametric equations of a line passing through the points A(3, 4, -7) and B(1, -1, 6) are

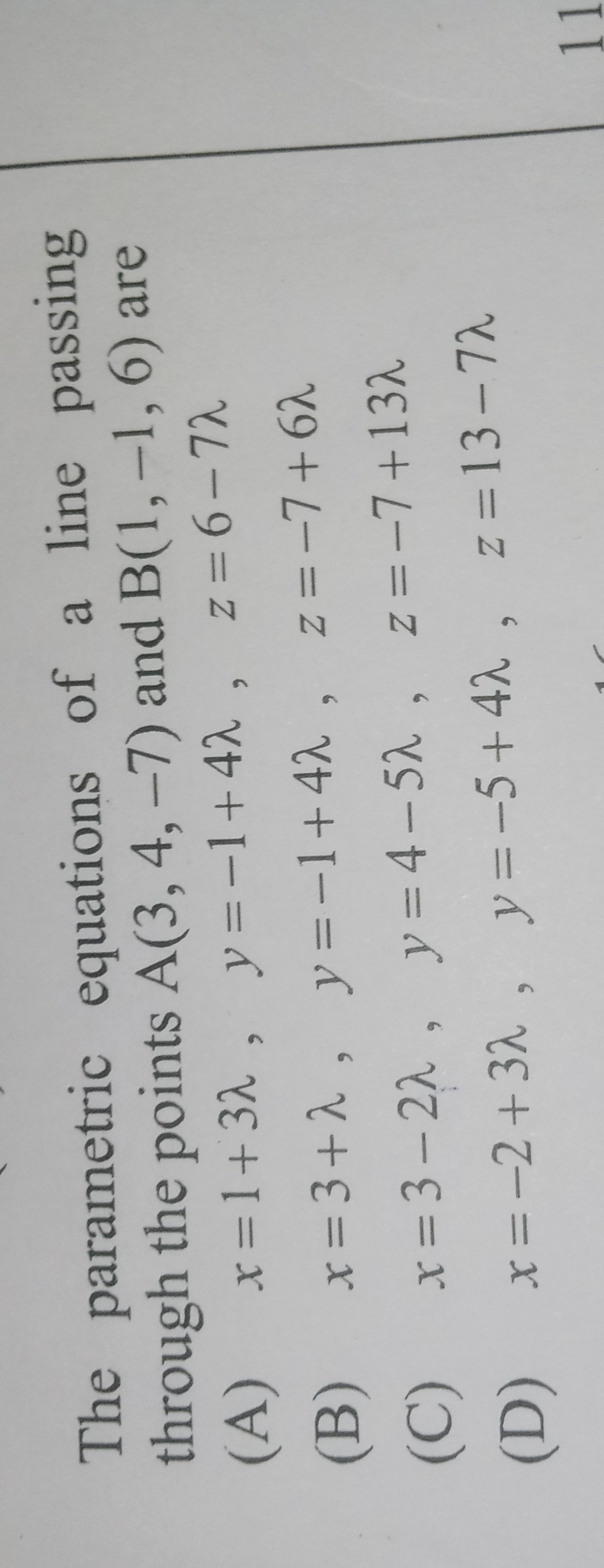
• A. $x=1+3\lambda$, $y=-1+4\lambda$, $z=6-7\lambda$
• B. $x=3+\lambda$, $y=-1+4\lambda$, $z=-7+6\lambda$
• C. $x=3-2\lambda$, $y=4-5\lambda$, $z=-7+13\lambda$
• D. $x=-2+3\lambda$, $y=-5+4\lambda$, $z=13-7\lambda$

Answer 1

Answer: (C)

Option (C) matches the derived equations.

Answer 2

To find the parametric equations of a line passing through two points A and B:

1. Find the direction vector: Subtract the coordinates of point A from point B to get the direction vector $\vec{d}$.

   $\vec{d} = B - A = (1-3, -1-4, 6-(-7)) = (-2, -5, 13)$

2. Write the parametric equations: Use point A (3, 4, -7) and the direction vector (-2, -5, 13) to form the equations:

   $x = 3 - 2\lambda$

   $y = 4 - 5\lambda$

   $z = -7 + 13\lambda$

Therefore, the correct answer is option (C).