Question

The parallax of distant planets as measured from two diametrically opposite ends of earth is $1$ minute. The distance of planet from the earth is (given radius of the earth =$6400km$ )
$\begin{aligned} & A)6.8\times {{10}^{10}}m \\\ & B)4.4\times {{10}^{10}}m \\\ & C)2.2\times {{10}^{10}}m \\\ & D)8.4\times {{10}^{8}}m \\\ \end{aligned}$

Answer 1

By parallax method the distance of a distant planet from the earth can be measured. First we need to convert the angle in minutes to radian, then we will apply the formula to calculate the distance with the help of the distance between the two diametrically opposite ends of earth. Let’s start with our solution.

Complete answer:
The diagram for the problem is drawn, where $d$ is the distance of the distant planet and $b$ is the distance between the two diametrically opposite ends of earth and $\theta$ is the parallax.

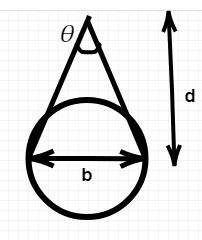
Here
$b=2\times 6400km=12800km$ and
$\theta =\dfrac{\pi }{180}\times \dfrac{1}{60}rad$. Now as $d$ is very large compared to $b$, we can write
$\begin{aligned} & \sin \theta =\theta =\dfrac{b}{d} \\\ & \Rightarrow d=\dfrac{b}{\theta } \\\ \end{aligned}$
Now putting the values of different quantities, we get
$\begin{aligned} & d=12800\times \dfrac{60\times 180}{\pi } \\\ & \Rightarrow d=4.4\times {{10}^{7}}km \\\ \end{aligned}$

So, the correct answer is “Option B”.

Additional Information:
Parallax is defined as the apparent shift of a body with respect to another, with the shift of eye. The distance between planets and stars from the earth cannot be measured directly with a meter scale. Hence an indirect method called parallax method is used.

Note:
To understand parallax, hold a pencil vertically in front of you at a certain distance against a point on a background like a wall. Now view the pencil with your right eye keeping the left eye closed and then with your left eye keeping the right eye closed. You will see with respect to the background point the position of the pencil shifts. This phenomenon is known as parallax. We must convert the angle in radian to get the right answer.