Question

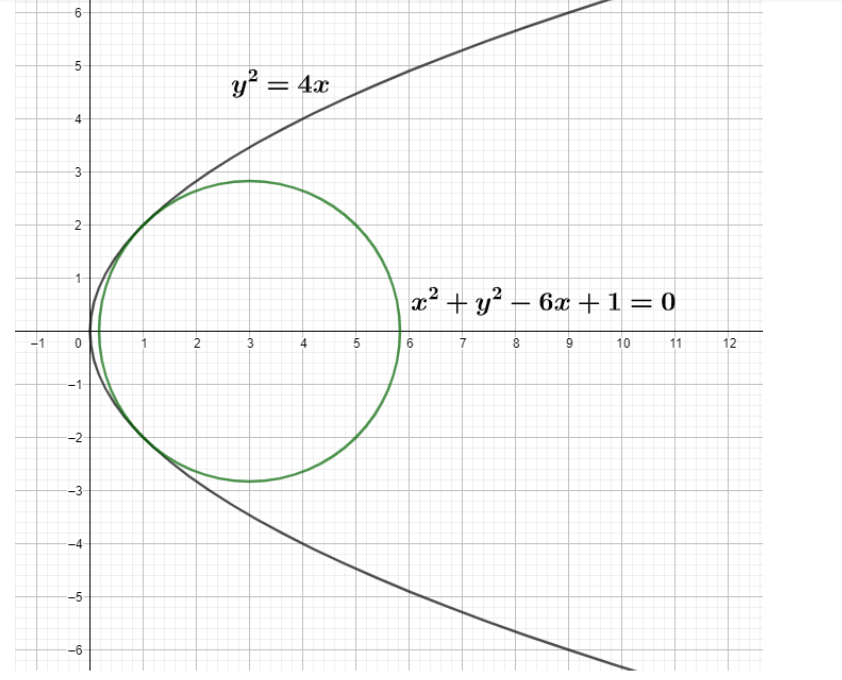
The parabola ${{y}^{2}}=4x$ and the circle ${{x}^{2}}+{{y}^{2}}-6x+1=0$ will
(A) Intersect at exactly one point
(B) Touch each other at two distinct points
(C) Touch each other at exactly one point
(D) Intersect each other at two distinct points.

Answer 1

Hint : In this question, we will first solve the given equations of two curves for the values of x and y by the substitution method. At the point of intersection, the coordinates of x and y will satisfy both the equations of curves of parabola and circle. If the tangent of both curves is the same at the point of intersection, then this implies that both curves touch each other.

Complete step-by-step answer :
When two curves intersect each other then, the coordinates of the point of intersection satisfies the equation of both the curves. This point of intersection is given by solving the two equations.
Equation of Parabola, ${{y}^{2}}=4x$ _ _ _ _ _ _ _ _(1)
Equation of Circle, ${{x}^{2}}+{{y}^{2}}-6x+1=0$ _ _ _ _ _ _ _ _(2)
We solve the two equation by substituting value of ${{y}^{2}}$from equation (1) in equation (2)
${{x}^{2}}+4x-6x+1=0$
Simplifying the equation,
${{x}^{2}}-2x+1=0$
${{x}^{2}}-x-x+1=0$factoring the equation, we get,
$\left( x-1 \right)\left( x-1 \right)=0$
This implies, $x=1$
Now, substituting value of x in equation (1), we get,
${{y}^{2}}=4\left( 1 \right)$
Taking square root in both the sides of equation, we get,
$y=\sqrt{4}$
$y=\pm 2$
So, the given two curves will meet at two points, that is, $\left( 1,2 \right)$and $\left( 1,-2 \right)$.
If the tangent of both curves is same at the points where they meet, then this implies that they will touch each other at that point otherwise they will intersect at that point.
The tangent of the curve is given by differentiating the equation of the given curve. So,
Equation of tangent of Parabola
${{y}^{2}}=4x$
Differentiating both sides with respect to x
$2y\dfrac{dy}{dx}=4$
$\dfrac{dy}{dx}=\dfrac{4}{2y}$
$\dfrac{dy}{dx}=\dfrac{2}{y}$
Equation of tangent of Circle
${{x}^{2}}+{{y}^{2}}-6x+1=0$
Differentiating both sides with respect to x
$2x+2y\dfrac{dy}{dx}-6+0=0$
$2y\dfrac{dy}{dx}=6-2x$
$\dfrac{dy}{dx}=\dfrac{6-2x}{2y}$
$\dfrac{dy}{dx}=\dfrac{3-x}{y}$
At $\left( 1,2 \right)$
Tangent of Parabola, $\dfrac{dy}{dx}=\dfrac{2}{2}=1$
Tangent of Circle, $\dfrac{dy}{dx}=\dfrac{3-1}{2}=\dfrac{2}{2}=1$
Tangent of Parabola = Tangent of Circle at $\left( 1,2 \right)$
So, the two curves, that is, Parabola and Circle meet each other at $\left( 1,2 \right)$
At $\left( 1,-2 \right)$
Tangent of Parabola, $\dfrac{dy}{dx}=\dfrac{2}{-2}=-1$
Tangent of Circle, $\dfrac{dy}{dx}=\dfrac{3-1}{-2}=\dfrac{2}{-2}=-1$
Tangent of Parabola = Tangent of Circle at $\left( 1,-2 \right)$
So, the two curves, that is, Parabola and Circle meet each other at $\left( 1,-2 \right)$.
This implies the two curves will touch each other at two distinct points.
Hence, option (B) is the correct answer.

So, the correct answer is “Option B”.

Note : The main thing to keep in mind is that when two curves meet each other then there are two possibilities, either, they intersect each other or they just meet each other or they touch each other. We have to check by finding the tangent at the point where they meet. If the tangent of both curves is the same at the point where they meet, then they touch each other otherwise they will intersect each other. Take care while doing the calculations.