Question

The pair of equations $x=a$ and $y=b$ graphically represents lines which are:
A.Parallel
B.Intersecting at $\left( b,a \right)$
C.Coincident
D.Intersecting at $\left( a,b \right)$

Answer 1

Hint: The $x$ coordinate of a point determines its distance from the $y$ axis and the $y$ coordinate of the point determines its distance from the $x$ axis . A line parallel to the $x$ axis is of the form $y=c$ and a line parallel to the $y$ axis is of the form $x=c$ , where $c$ is any constant.

Complete step-by-step answer:
Before plotting the points , we must know about the coordinate system.
The cartesian coordinate system is a system of identifying the location of a point with respect to two perpendicular lines , known as coordinate axes. The vertical axis is called the $y$ axis and the horizontal axis is called the $x$ axis. The point of intersection of these axes is called the origin and it is represented by the ordered pair $(0,0)$. The distance of a point from the $y$ axis is called the $x$coordinate and the distance of the point from $x$ axis is called the $y$ coordinate of the point. The equation of a line passing through a point $\left( {{x}_{1}},{{y}_{1}} \right)$ is given as $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$ , where $m$ is the slope of the line. Now, if the line is parallel to the $x$ axis, then its slope is equal to zero . So, the equation of the line will be $y-{{y}_{1}}=0$ . So, the $y$ coordinate of any point on the line will be ${{y}_{1}}$. Similarly, if the line is parallel to the $y$ axis, then the slope of the line will be equal to infinity, and the equation of the line will be of the form $x-{{x}_{1}}=0$ . So, the $x$ coordinate of any point on the line will be ${{x}_{1}}$.
Now, coming to the question, the pair of equations given to us are $x=a$ and $y=b$. The equation $x=a$ is of the form $x-{{x}_{1}}=0$ , and hence, represents a line parallel to $y$ axis at a distance of $a$ units from it. Similarly, the equation $y=b$ is of the form $y-{{y}_{1}}=0$ , and hence, represents a line parallel to the $x$ axis at a distance of $b$ units from it. Hence, the two lines are perpendicular and therefore, will intersect at a point. Now, any point on the line $x=a$ will have its $x$ coordinate equal to $a$ and any point on the line $y=b$ will have its $y$ coordinate equal to $b$ . So, the coordinates of the point of intersection of the lines $x=a$ and $y=b$ will be $\left( a,b \right)$ .

This can be represented graphically as:

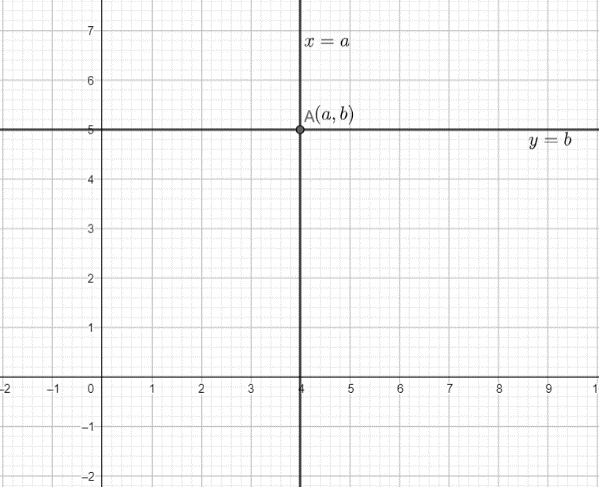
So, the lines $x=a$ and $y=b$ are intersecting lines and they intersect at the point $\left( a,b \right)$.
Hence, option D. is the correct option.

Note: Students get confused and write that the line $x=a$ is parallel to the $x$ axis , which is wrong. Such confusion should be avoided.