Question

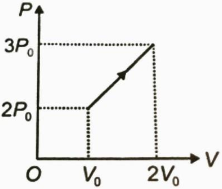
The $P-V$ graph for a monatomic gas is shown in figure. Find the energy absorbed by the gas during the process.

Answer 1

"Monatomic" is a combination of the words "mono" and "atomic" in physics and chemistry, and it implies "one atom." It's most commonly used to describe gases: a monatomic gas is one in which the atoms are not connected to one another. The noble gases argon, krypton, and xenon are examples at standard settings, yet at sufficiently high temperatures, all chemical elements will be monatomic in the gas phase. Because it has no rotational or vibrational energy, the thermodynamic behaviour of a monatomic gas is exceedingly simple when compared to polyatomic gases.

Complete step by step answer:
According to the Ideal gas law,
$PV = nRT$
where, $P$ , $V$ and $T$ are the pressure, volume and temperature; $n$ is the amount of substance; and $R$ is the ideal gas constant.
Now,
$nR = \dfrac{{PV}}{T} \\\ \Rightarrow nR = \dfrac{{{P_A}{V_A}}}{{{T_A}}} = \dfrac{{{P_B}{V_B}}}{{{T_B}}} \\\$
$\Rightarrow {T_B} = \dfrac{{{P_B}{V_B}{T_A}}}{{{P_A}{V_A}}} \\\ \Rightarrow {T_B}= \dfrac{{3{P_0} \cdot 2{V_0} \cdot {T_0}}}{{2{P_0} \times {V_0}}} \\\ \Rightarrow {T_B}=3{T_0} \\\ \because {T_A} = {T_0} \\\$
And, we need to find ;
$\Delta Q = \Delta U + \Delta W$ [The first law of thermodynamics is this.]
The heat provided to the system by the environment is denoted by $\Delta Q$ . $\Delta W$ denotes the amount of work done by the system in relation to the environment. The change in the system's internal energy is denoted by $\Delta U$ . Some of the heat given is wasted, while the remainder is used to act on the environment.
$\Delta U = n{C_V}\Delta T \\\ \Rightarrow \Delta U = n \times \dfrac{3}{2}R \times \left( {{T_B} - {T_A}} \right) \\\ \Rightarrow \Delta U = nR \times \dfrac{3}{2} \times \left( {3{T_0} - {T_0}} \right) \\\ \Rightarrow \Delta U = \dfrac{{{P_A}{V_A}}}{{{T_A}}} \times \dfrac{3}{2} \times 2{T_0} \\\ \Rightarrow \Delta U = \dfrac{{2{P_0} \times {V_0}}}{{{T_0}}} \times \dfrac{3}{2} \times 2{T_0} \\\ \Rightarrow \Delta U = 6{P_0}{V_0} \\\$
Also, $\Delta W$= area under the graph
$\Delta W = \dfrac{1}{2} \times {V_0} \times {P_0} + {V_0} \times 2{P_0} \\\ \Rightarrow \Delta W= 2.5{P_0}{V_0} \\\$
$\Rightarrow \Delta Q = 6{P_0}{V_0} + 2.5{P_0}{V_0} \\\ \therefore \Delta Q= 8.5{P_0}{V_0} \\\$
As a result, the gas absorbs energy during the process $\Delta Q = 8.5{P_0}{V_0}$.

Note: An atom in a monatomic gas can travel in three directions independently, the gas possesses three degrees of freedom due to its translational motion. As a result, the equation $U{\text{ }} = \dfrac{3}{2}RT$ applies to its internal energy, $U$ . The heat capacity at constant volume, ${C_V}$ , is the temperature-dependent derivative of the internal energy, therefore ${C_V}{\text{ }} = {\text{ }}\dfrac{3}{2}R$ for our monoatomic gas.