Question

The oxidation potential (in volt) of a hydrogen electrode at pH = 7 and $p_{H_2}$ = 1 atm is

$\left( \text{Given } 2.303 \frac{RT}{F} = 0.06 \right)$

Answer 1

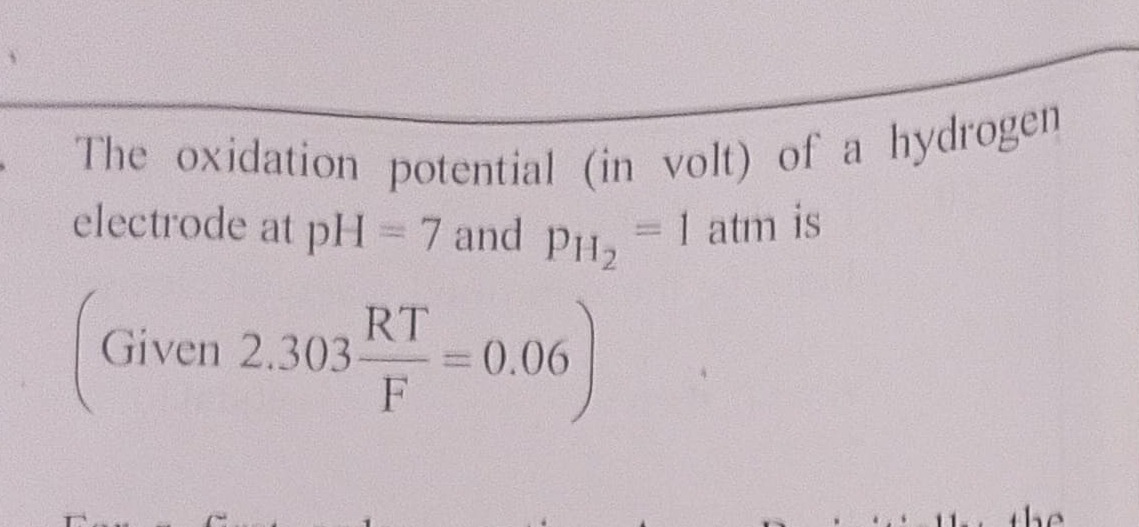
0.42

Answer 2

To find the oxidation potential of a hydrogen electrode, we first write the oxidation half-reaction and then apply the Nernst equation.

1. Oxidation Half-Reaction: The oxidation of hydrogen gas to hydrogen ions is represented as: $\frac{1}{2}H_2(g) \rightleftharpoons H^+(aq) + e^-$ For this reaction, the number of electrons transferred, $n = 1$. The standard oxidation potential for a hydrogen electrode, $E^0_{ox}$, is 0 V.

2. Nernst Equation: The Nernst equation for the oxidation potential ($E_{ox}$) is: $E_{ox} = E^0_{ox} - \frac{2.303 RT}{nF} \log \frac{\text{[Product]}}{\text{[Reactant]}}$ Substituting the species from the half-reaction: $E_{ox} = E^0_{ox} - \frac{2.303 RT}{nF} \log \frac{[H^+]}{p_{H_2}^{1/2}}$

3. Given Values:

• $E^0_{ox} = 0$ V
• $n = 1$
• $2.303 \frac{RT}{F} = 0.06$ (given)
• pH = 7
• $p_{H_2} = 1$ atm

4. Calculate $[H^+]$ from pH: pH = $-\log[H^+]$ $7 = -\log[H^+]$ $\log[H^+] = -7$ $[H^+] = 10^{-7}$ M

5. Substitute values into the Nernst Equation: $E_{ox} = 0 - \frac{0.06}{1} \log \frac{10^{-7}}{(1)^{1/2}}$ $E_{ox} = -0.06 \log (10^{-7})$ Using the property $\log(a^b) = b \log(a)$: $E_{ox} = -0.06 \times (-7) \log(10)$ Since $\log(10) = 1$: $E_{ox} = -0.06 \times (-7)$ $E_{ox} = 0.42$ V

The oxidation potential of the hydrogen electrode at pH = 7 and $p_{H_2}$ = 1 atm is 0.42 V.