Question
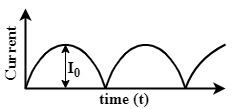
Question: The output sinusoidal current versus time graph of a rectifier is shown in the figure. The average v...
The output sinusoidal current versus time graph of a rectifier is shown in the figure. The average value of output current:
a) 0
b) 2I0
c) 4I0
d) None of these
Solution
A rectifier is an electrical device that converts any AC sinusoidal signal into a one directional DC signal. The sinusoidal signal still remains sinusoidal but the negative portion reverses its direction and current only flows in one direction as shown in the graph.
Formula used:
Time average of any sinusoidal function is given by:
fav=∫0Tdt∫0Tf(t)dt...................(1)
Where,
favis the time average of the sinusoidal function,
T is the time period of the function,
f(t)is the sinusoidal function.
Step by step answer:
Given:
From the given graph we get the given current function as:
I(t)=I0sinωt0⩽t⩽2T =−I0sinωt2T<t⩽T ......................(2)
Where, time period T is given by T=ω2π.
To find: Average value of output current.
Step 1
First, use the current function from eq.(2)and value of T to get the numerator of eq.(1) as:
∫0TI(t)dt=∫0ωπI0sinωtdt+∫ωπω2π−I0sinωtdt
=ωI0[−cosωt]0ωπ−ωI0[−cosωt]ωπω2π
=ωI0[−(−1)−(−1)]−ωI0[(−1)−1]
=ω4I0
Step 2
Now, use the value of T to calculate the denominator of eq.(1) as:
Step 3
From the obtained value of the numerator and denominator get the average current as:
Iav=∫0Tdt∫0TI(t)dt ∴Iav=ω2πω4I0=π2I0
Correct answer:
The average value of output current is given by (d) none of these.
Note: This problem can be solved in a tricky way. Notice, the sinusoidal function of eq.(2). From the given current function you’ll get the numerator a real value times I0 from the integration of the sine function. Since, the time period is given by ω2π so after integration the denominator will consist of the term π. In the first three given options there is no term involving π in its denominator. Hence, the option must be option (d) and you can get that without a single calculation.
