Question

The orthocentre of the triangle formed by the pair of lines $2x^2 - xy - y^2 + x + 2y - 1 = 0$ and the line $x + y + 1 = 0$ is:

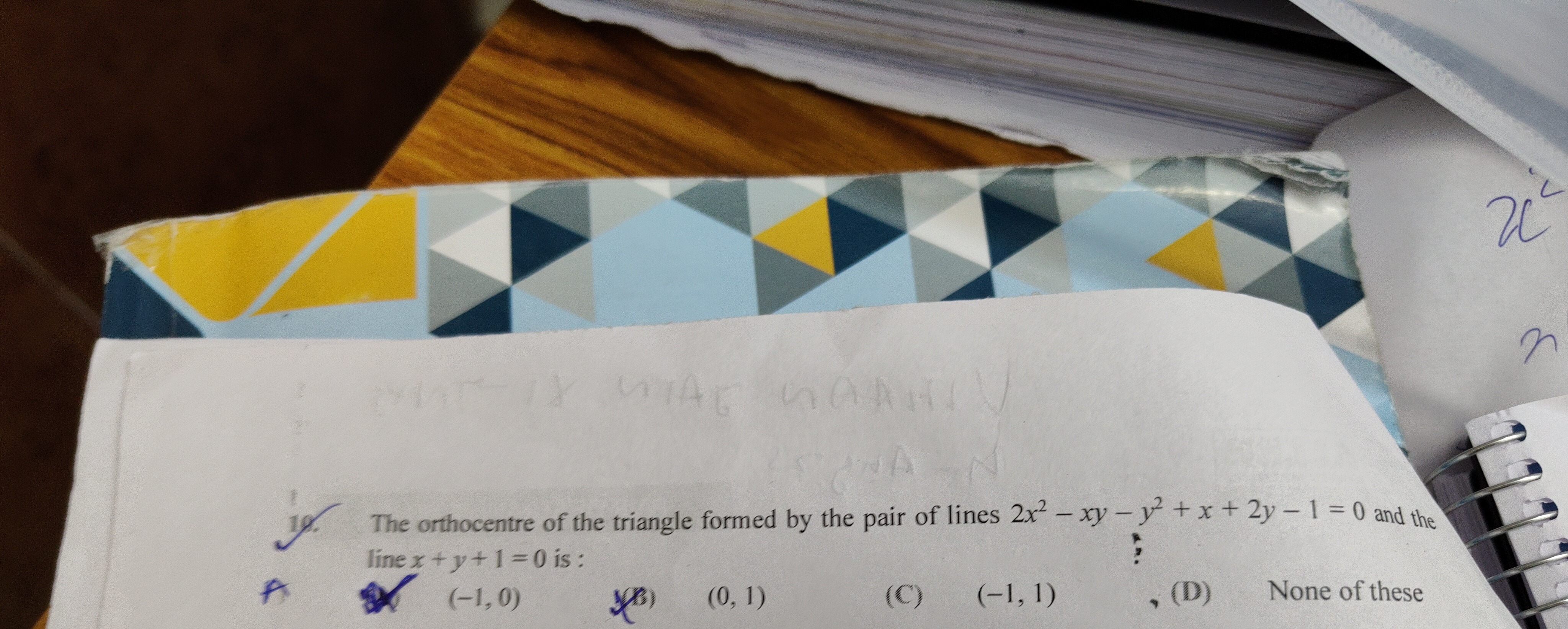
• A. (-1, 0)
• B. (0, 1)
• C. (-1, 1)
• D. None of these

Answer 1

Answer: (A)

(-1, 0)

Answer 2

1. Decompose the given quadratic equation $2x^2 - xy - y^2 + x + 2y - 1 = 0$ into two linear equations $L_1: 2x+y-1=0$ and $L_2: x-y+1=0$.
2. Identify the third line $L_3: x+y+1=0$.
3. Calculate the vertices of the triangle by finding the intersection points of these lines: $V_1 = L_1 \cap L_2 = (0,1)$, $V_2 = L_1 \cap L_3 = (2,-3)$, $V_3 = L_2 \cap L_3 = (-1,0)$.
4. Determine the slopes of the sides: $m(V_1V_2)=-2$, $m(V_2V_3)=-1$, $m(V_3V_1)=1$.
5. Observe that $m(V_2V_3) \times m(V_3V_1) = (-1) \times 1 = -1$, indicating that the triangle is right-angled at $V_3(-1,0)$.
6. The orthocentre of a right-angled triangle is the vertex where the right angle is formed. Therefore, the orthocentre is $V_3(-1,0)$.

Alternatively, find the equations of two altitudes.

• Altitude from $V_1(0,1)$ is perpendicular to $V_2V_3$ (slope -1), so its slope is 1. Equation: $y-1=1(x-0) \implies x-y+1=0$ ($L_2$).
• Altitude from $V_2(2,-3)$ is perpendicular to $V_3V_1$ (slope 1), so its slope is -1. Equation: $y-(-3)=-1(x-2) \implies x+y+1=0$ ($L_3$).
• The intersection of altitudes $L_2$ and $L_3$ is $(-1,0)$, which is the orthocentre.