Question

The orthocentre of $\Delta ABC$ if $A\left( \cos {{\theta }_{1}},\sin {{\theta }_{1}} \right),B\left( \cos {{\theta }_{2}},\sin {{\theta }_{2}} \right),C\left( \cos {{\theta }_{3}},\sin {{\theta }_{3}} \right)$ is
A. $\left( \dfrac{\sum{\cos {{\theta }_{1}}}}{2},\dfrac{\sum{\sin {{\theta }_{1}}}}{2} \right)$
B. $\left( \dfrac{\sum{\cos {{\theta }_{1}}}}{3},\dfrac{\sum{\sin {{\theta }_{1}}}}{3} \right)$
C. $\left( \sum{\cos {{\theta }_{1}}},\sum{\sin {{\theta }_{1}}} \right)$
D. Data insufficient

Answer 1

To solve this problem, we should first find out the circumcentre of the triangle and then use the relation between circumcentre, orthocentre and centroid. If we observe the coordinates of all the points, we know that, for any value of $\theta$,${{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1$, all the points of the triangle lie on the circle ${{x}^{2}}+{{y}^{2}}=1$. So, the circle ${{x}^{2}}+{{y}^{2}}=1$ and the point $O\left( 0,0 \right)$ are the circumcircle and the circumcentre of the triangle respectively. We know that the centroid of the triangle $D\left( {{x}_{1}},{{y}_{1}} \right),E\left( {{x}_{2}},{{y}_{2}} \right),F\left( {{x}_{3}},{{y}_{3}} \right)$ is given by $G\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$. Using this, we can calculate the centroid of the triangle. A point $C\left( x,y \right)$ dividing the line joining $D\left( {{x}_{1}},{{y}_{1}} \right),E\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio $m:n$ is given by $\left( x,y \right)=\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$. Using the property that centroid divides the line joining the orthocentre and circumcentre in the ratio $2:1$, we can get the coordinates of the orthocentre.

Complete step-by-step answer :


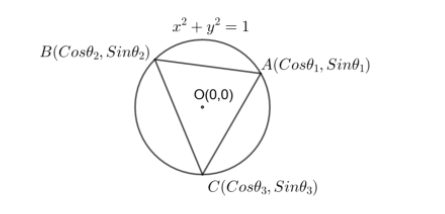
We are given the triangle $\Delta ABC$ with the coordinates of A, B, C as
$A\left( \cos {{\theta }_{1}},\sin {{\theta }_{1}} \right),B\left( \cos {{\theta }_{2}},\sin {{\theta }_{2}} \right),C\left( \cos {{\theta }_{3}},\sin {{\theta }_{3}} \right)$.
We know the relation between $\cos \theta$ and $\sin \theta$ as ${{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1$.
Using this, we can come to a conclusion that the three points A, B, C satisfy the equation ${{x}^{2}}+{{y}^{2}}=1$.
The equation ${{x}^{2}}+{{y}^{2}}=1$ is a circle with centre at $O\left( 0,0 \right)$.
As the three vertices lie on the circle, they are equidistant from the point $O\left( 0,0 \right)$.
The circumcentre is a point which is equidistant from the three vertices of the triangle. Using this, we can conclude that $O\left( 0,0 \right)$ is the circumcentre of the circle.
We know that the centroid of the triangle $D\left( {{x}_{1}},{{y}_{1}} \right),E\left( {{x}_{2}},{{y}_{2}} \right),F\left( {{x}_{3}},{{y}_{3}} \right)$ is given by $G\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$.
Centroid of the triangle ABC is
$G\left( \dfrac{\cos {{\theta }_{1}}+\cos {{\theta }_{2}}+\cos {{\theta }_{3}}}{3},\dfrac{\sin {{\theta }_{1}}+\sin {{\theta }_{2}}+\sin {{\theta }_{3}}}{3} \right)$
A point $C\left( x,y \right)$ dividing the line joining $D\left( {{x}_{1}},{{y}_{1}} \right),E\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio $m:n$ is given by $\left( x,y \right)=\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$.

We know the property that centroid divides the line joining the orthocentre and circumcentre in the ratio $2:1$.
Here
C- Centroid$\left( x,y \right)=\left( \dfrac{\cos {{\theta }_{1}}+\cos {{\theta }_{2}}+\cos {{\theta }_{3}}}{3},\dfrac{\sin {{\theta }_{1}}+\sin {{\theta }_{2}}+\sin {{\theta }_{3}}}{3} \right)$
D-Orthocentre$=H\left( {{x}_{1}},{{y}_{1}} \right)$
E-Circumcentre$=O\left( 0,0 \right)=\left( {{x}_{2}},{{y}_{2}} \right)$
m = 2
n = 1
Applying the formula with orthocentre being $H\left( {{x}_{1}},{{y}_{1}} \right)$, we get

& \left( \dfrac{\cos {{\theta }_{1}}+\cos {{\theta }_{2}}+\cos {{\theta }_{3}}}{3},\dfrac{\sin {{\theta }_{1}}+\sin {{\theta }_{2}}+\sin {{\theta }_{3}}}{3} \right)=\left( \dfrac{2\times 0+1\times {{x}_{1}}}{2+1},\dfrac{2\times 0+1\times {{y}_{1}}}{2+1} \right) \\\ & \left( \dfrac{\cos {{\theta }_{1}}+\cos {{\theta }_{2}}+\cos {{\theta }_{3}}}{3},\dfrac{\sin {{\theta }_{1}}+\sin {{\theta }_{2}}+\sin {{\theta }_{3}}}{3} \right)=\left( \dfrac{{{x}_{1}}}{3},\dfrac{{{y}_{1}}}{3} \right) \\\ & \left( \cos {{\theta }_{1}}+\cos {{\theta }_{2}}+\cos {{\theta }_{3}},\sin {{\theta }_{1}}+\sin {{\theta }_{2}}+\sin {{\theta }_{3}} \right)=\left( {{x}_{1}},{{y}_{1}} \right) \\\ \end{aligned}$$ $\therefore$ The coordinates of the orthocentre H are $\left( \sum{\cos {{\theta }_{1}}},\sum{\sin {{\theta }_{1}}} \right)$. The answer is option-C. **Note** : The trick in the question is to find that the circumcentre of the triangle is origin $O\left( 0,0 \right)$. Some students will do the regular process to find the orthocentre by finding the perpendicular line to BC passing through A. That process will be very lengthy. In these kind of questions where $\cos \theta $ and $\sin \theta $ are involved, we should be aware that $${{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1$$ and this has led to a conclusion that the three points lie on the circle ${{x}^{2}}+{{y}^{2}}=1$.