Question

The Orthocenter of a triangle is the point where………….
(A) the medians meet
(B) the altitudes meet
(C) the right bisectors of the sides of the triangle meet
(D) the bisectors of the angles of the triangle meet

Answer 1

Hint: Take a $\Delta ABC$ and then draw the altitudes to the side AB, BC, and AC. We can see that these three altitudes meet at point O and point O coincides with the orthocenter of the triangle. Now, conclude the answer.

Complete step by step solution:

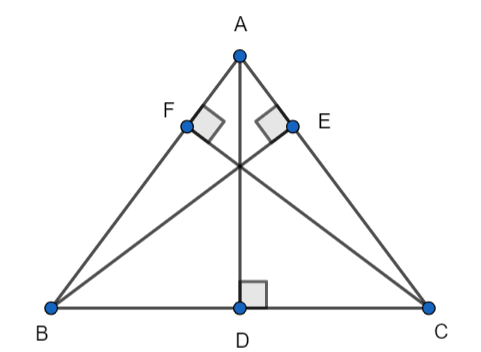
In the $\Delta ABC$, we have AB, BC, and AC as the sides of the triangle.
The line drawn from point A which is touching the side BC at point D is perpendicular to the base BC of the triangle. It means that AD is the altitude to the side BC.
The line drawn from point B which is touching the side AC at point E is perpendicular to the side AC of the triangle. It means that BE is the altitude to the side AC.
The line drawn from point C which is touching the side BC at point D is perpendicular to the base BC of the triangle. It means that CF is the altitude to the side AB.
The line AD, BE, and CF is the perpendicular lines which are meeting at the point O. In other words, we can say that the point of intersection of the altitudes is point O.
We know that the point where the altitudes or the perpendicular lines meet coincides with the orthocenter.
Therefore, the orthocenter is the point where the altitudes meet.
Hence, option A is the correct option.

Note: In this question, one might get confused and go with option (A) which says that the orthocenter is the point of intersection of medians. This is wrong. The orthocenter is the point of intersection of the altitudes. The best way to overcome this mistake is to keep in mind that wherever the term ortho comes in maths it is somewhat related to the perpendiculars or altitudes.