Question

The orbital angular momentum of an electron ($l = 1$) makes an angle of ${\text{4}}{{\text{5}}^{\text{o}}}$from $Z$ axis. The ${{\text{L}}_{\text{z}}}$ of electron will be
(${{\text{L}}_{\text{Z}}}{\text{ = }}\,{\text{m}}\dfrac{{\text{h}}}{{{{2\Pi }}}}$)
A.${\text{2}} \times \dfrac{{\text{h}}}{{{{2\Pi }}}}$
B.${\text{0}} \times \dfrac{{\text{h}}}{{{{2\Pi }}}}$
C.${\text{3}}\dfrac{{\text{h}}}{{{{2\Pi }}}}$
D.${\text{3}} \times \dfrac{{\text{h}}}{{{{2\Pi }}}}$

Answer 1

When the Schrodinger equation is solved for the hydrogen atom ,it is found that there are 3 characteristic quantum numbers $n\,,\,l\,,\,m$ which represent an orbital in the hydrogen atom. $n$ is the principal quantum number , $l$ is the orbital/azimuthal quantum number, $m$ is the magnetic quantum number.
For an atom containing more than one electron we need a fourth quantum number called spin quantum number represented by $s$, it is used to distinguish between two electrons in an orbital.

Complete answer:
When we look at the 4 quantum numbers
$n$ is the principal quantum number which represents the principal energy level of an otherwise shell in which the electron revolves around the nucleus. It can have any integral value other than zero, $n\, = \,1,2,3,4...........$
$l$ is the orbital quantum number also known as azimuthal quantum number which determines the subshell to which the electron belongs . For a $n$ value $l$can have values $0 \to n - 1$.
$m$ is the magnetic quantum number representing the orientation of atomic orbital in space , which depend on the values of $l$, so it can have values ($2l + 1$)
$s$ is the spin quantum number which represent spin of electron its value is $\pm \dfrac{1}{2}$
Now we can learn about angular momentum. Angular momentum is a physical quantity which plays an important role in understanding the electronic structure of an atom. Here we can consider the hydrogen atom as an example in which the electron in the hydrogen atom moves in a circular orbit with constant speed / angular velocity.

So any moving object with mass , possess momentum . so angular momentum deals with rotating or spinning objects.
Angular momentum can be calculated by using formula
$L = I\omega$ where $I$ is the moment of inertia and $\omega$is the angular velocity
For a particle of mass $m$ moving in a circle of radius $r$
$I\, = \,\,m\,{r^2}$ , $\omega \, = \,\dfrac{v}{r}$ where $v$ is the velocity of moving particles.
$L\, = \,mvr$
And the orbital angular momentum of a single electron is given by the equation
$L\, = \sqrt {l\left( {l + 1} \right)} \,\dfrac{h}{{2\Pi }}$ where $l$ is the orbital angular momentum quantum number.
$z$ component of orbital angular momentum is given by the equation
${L_Z} = m\dfrac{h}{{2\Pi }}$ where $m$ is the magnetic moment quantum number.
Complete step by step solution: it has clearly written as $l = 1$ so here the electron is in $p$ subshell. Here movement of an electron in an orbital makes an angle of ${45^o}$ from the ${L_{_Z}}$axis in the $xy\,$plane.

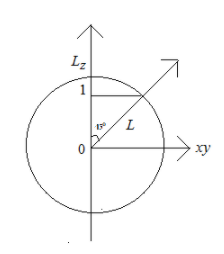
Orbital angular momentum is given by the equation $L\, = \,\sqrt {l\left( {l + 1} \right)} \,\dfrac{h}{{2\Pi }}$
Here $l = 1$ ,then we get $L = \sqrt {1\left( {1 + 1} \right)} \dfrac{h}{{2\Pi }}\, = \sqrt {2\,} \dfrac{h}{{2\Pi }}$
Here we have to calculate orbital angular momentum in ${L_Z}$axis
From the above figure ${\text{Cos}}\,\,{{\theta }}\, = \,\dfrac{{{L_Z}}}{L}$
So we get ${L_Z}\, = \,L\,\cos \theta$,where $\theta = \,{45^0}$ hence the value of $\operatorname{Cos} \theta \, = \,\sqrt 2$
$\therefore \,{L_Z}\, = \,\sqrt 2 \dfrac{h}{{2\Pi }} \times \,\sqrt 2 \, = \dfrac{h}{{2\Pi }}$

So, here the correct answer is option C .

Note:
It has to be noted that each electron in an atom has a unique set of quantum numbers , that is according to Pauli's exclusion principle no two electrons in an atom can have the same set of four quantum numbers.