Question

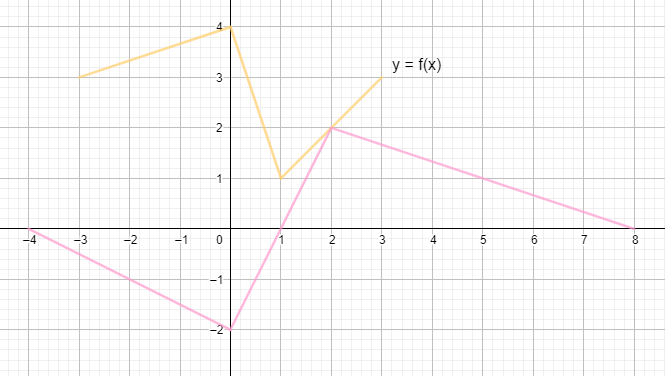
The orange graph is the function $f\left( x \right)$. How do you describe the transformations on the pink graph and write an equation for it?

Answer 1

In this question we have been given with two graphs on different colors which we have to compare and then write an equation for the pink graph by making appropriate transformations. We will first see the various similarities and differences between the two graphs and then calculate the horizontal and vertical dilation on the graphs and the shift factor. We will then write the equation in the form of a function.

Complete step-by-step solution:
We can observe from the graph that the pink graph is wider than the orange graph which implies there is horizontal dilation.
We can see that the vertical height of both the graphs is the same therefore there will be no changes in the function for that.
The pink graph is lower than the orange graph which indicates a vertical translation.
Now the ratio of the widths on the orange graph is $3:1:2$ and in the pink graph it is $4:2:6$, since no transformation can convert $3:1:2$ to $4:2:6$, we will use the horizontal flip method which is that we can convert $3:1:2$ into the reverse of $4:2:6$, which is $6:2:4$, therefore there is a horizontal dilation by a factor of $2$.
Now since we are taking the reverse, the function $f\left( x \right)$ becomes $f\left( -x \right)$ and stretching it by a factor of $2$, we get $f\left( -\dfrac{x}{2} \right)$.
Since there is a translation to the right by a factor of $2$, we get the function as $f\left( -\dfrac{\left( x-2 \right)}{2} \right)$
And to move the orange graph to the pink graph there has to be a translation downwards by a factor of $3$ therefore, it can be written as $f\left( -\dfrac{\left( x-2 \right)}{2} \right)-3$.
Therefore, the required function is:
$y=f\left( -\dfrac{\left( x-2 \right)}{2} \right)-3$ to convert $y=f\left( x \right)$ from the orange graph to the pink graph using suitable transformations.

Note: Whenever there is a translation done by a factor towards the right or downwards, the value of the factor should be subtracted and whenever it is done towards the left or upwards, the value of the factor should be added. This type of problem can only be solved by the “trial and error method” . The similarities and differences should be seen and put together to get the required solution.