Question

The optical path difference between the two identical waves arriving at a point is $75.5\lambda$. Is the point bright or dark?
A) Bright
B) Dark
C) Neither bright nor dark
D) None of the above

Answer 1

The solution of the question lies in the experiment of Young’s double-slit experiment. In Young’s double-slit experiment the screen has two holes and another screen observes the bright and dark fringes. These bright and dark fringes are known by the formulas and properties. For bright fringes to be at ‘$Y$’, $\lambda$ must be equal to $YdD$ where $D$ is the distance of the screen and $d$ is the distance of holes. For bright $Y=n\lambda dD$ and for dark $Y=(n+1) \lambda$ dD

Complete step by step answer:
Step 1:
Before we start it is important to know what Young's double-slit experiment is. This is an experiment that brings out the bright and dark fringes from a source. This source is a beam of light or photons going through two holes equal to the wavelength that means the difference between the holes is very small and the fringes obtain on the other screen.

Step 2:
For better understanding and working of the experiment, there is a diagram below.

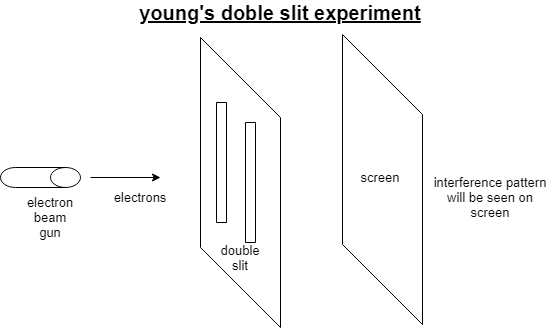
A labeled diagram is provided the distance between the slit is ‘d’ and the distance between the screens are D. An electron beam or beam of light or beam of photons in bombarded on the slits and according to their nature they produce interference pattern and fringes dark and bright obtain on screen
Working:
Young’s double-slit experiment uses two coherent sources of light placed at a small distance d slightly greater or equal to the wavelength of light. It helps in understanding the wave theory of light. The screen is placed at a distance $D$.
At any point on the screen at a distance ‘Y’ from the center, the waves travel distance ${l_1}$ and ${l_2}$ from holes 1 and 2. The path difference of $\Delta l$ is created by the points. The point subtends at an angle $\theta$ but D is very large so there is a very small difference of angle subtended at the source.

Step 3:
For constructive interference, the path difference must be an integral multiple of the wavelength
${Y_{nth}} = n \lambda Dd$ where, $D$ is distance of screen(large) and $d$ is distance of slits (very small) and also $n$ is the integral multiple
n=$\pm 0,1,2,3$ …(1)
for the dark or destructive fringes , $Y=\left( {n + 1} \right)\lambda dD$ ….(2)
Now we have given $75.5\lambda$ which can be written as $75 + \dfrac{1}{2}$ $\lambda$ ….(3)
Comparing Eqn(3) with Eqn(2) we can clearly state that it is the pattern of dark fringes or destructive fringes
Hence, we will obtain dark fringes with $75.5\lambda$

As the given wavelength is not an integral multiple of $n$, the point will be in the dark fringe. So, option B is correct.

Note:
Wave nature of light – The wave nature of light was given by James Clerk Maxwell in 1864. He led to the view that light is of electromagnetic nature, propagating as a wave from the source to the receiver. Heinrich Hertz discovered experimentally the existence of electromagnetic waves at radio frequencies.
The light behaves like a wave as it undergoes reflection, refraction, and diffraction just like any wave would go. In an electromagnetic wave, electric and magnetic field vectors are perpendicular to each other and at the same time are perpendicular to the direction of propagation of the wave. Hence we can say that the nature of these waves is transverse in nature.