Question

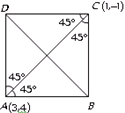
The opposite angular points of a square are $( 3,4 )$ and $( 1 , - 1 )$. Then the co-ordinates of other two points are.

• A. $D \left( \frac { 1 } { 2 } , \frac { 9 } { 2 } \right) , B \left( - \frac { 1 } { 2 } , \frac { 5 } { 2 } \right)$
• B. $D \left( \frac { 1 } { 2 } , \frac { 9 } { 2 } \right) , B \left( \frac { 1 } { 2 } , \frac { 5 } { 2 } \right)$
• C. $D \left( \frac { 9 } { 2 } , \frac { 1 } { 2 } \right) , B \left( - \frac { 1 } { 2 } , \frac { 5 } { 2 } \right)$
• D. None of these

Answer 1

Answer: (C)

$D \left( \frac { 9 } { 2 } , \frac { 1 } { 2 } \right) , B \left( - \frac { 1 } { 2 } , \frac { 5 } { 2 } \right)$

Answer 2

Obviously, slope of $A C = 5 / 2$ .

Let m be the slope of a line inclined at an angle of $45 ^ { \circ }$to AC, then $\tan 45 ^ { \circ } = \pm \frac { m - \frac { 5 } { 2 } } { 1 + m \cdot \frac { 5 } { 2 } } \Rightarrow m = - \frac { 7 } { 3 } , \frac { 3 } { 7 }$.

Thus, let the slope of AB or DC be 3/7and that of AD or BC be $- \frac { 7 } { 3 }$ . Then equation of AB is $3 x - 7 y + 19 = 0$.

Also the equation of BC is $7 x + 3 y - 4 = 0$.

On solving these equations, we get, $B \left( - \frac { 1 } { 2 } , \frac { 5 } { 2 } \right)$.

Now let the coordinates of the vertex D be (h, k). Since the middle points of AC and BD are same, therefore $\frac { 1 } { 2 } \left( h - \frac { 1 } { 2 } \right) = \frac { 1 } { 2 } ( 3 + 1 ) \Rightarrow h = \frac { 9 } { 2 }$, $\frac { 1 } { 2 } \left( k + \frac { 5 } { 2 } \right) = \frac { 1 } { 2 } ( 4 - 1 )$

⇒ $k = \frac { 1 } { 2 }$. Hence, $D = \left( \frac { 9 } { 2 } , \frac { 1 } { 2 } \right)$.