Question

The number of ways of choosing 2 squares $\left( {1 \times 1} \right)$ from a chess board so that they have exactly one common corner is ?
A. 98
B. 112
C. 36
D. 72

Answer 1

Hint:- Start with drawing a diagram of chess-board , now try to figure out which two $\left( {1 \times 1} \right)$ square will have only one common corner , you will find 1st square of 1st row and 2nd square of 2nd row will have only one common corner , similarly find for rest of the squares.

Complete step-by-step answer:
__
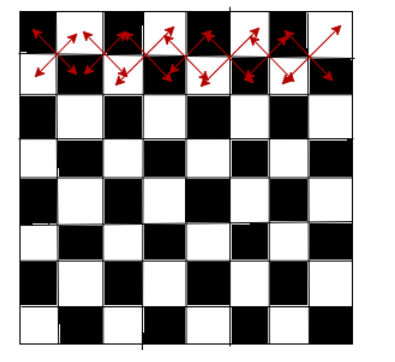
As we can see from the above figure, the chess board has 8 rows and 8 columns and a total of 64 $\left( {1 \times 1} \right)$.
So, now we have to choose two $\left( {1 \times 1} \right)$ squares such that they have exactly one common corner.
Now let us assume that we had to choose two $\left( {1 \times 1} \right)$ squares with one common corner from only the first two rows.
As all the possible pairs from row 1 and 2 are marked with arrows in the above figure.
So, we can see that there are 14 such pairs that exist in rows 1 and 2.
Now, all rows are the same , so each two consecutive rows will have 14 pairs of $\left( {1 \times 1} \right)$ squares with one common corner.
So, each of the rows (1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7) and (7, 8) will have 14 such pairs.
And, there are 7 pairs of rows.
So, the number of $\left( {1 \times 1} \right)$ squares with one common corner will be $7 \times 14 = 98$.
Hence, the correct option will be A.
Note:- Chess board is symmetric at all. So, if the number of one common corner square in two consecutive rows is 14. Then all consecutive rows will have the same number (i.e. 14) one common corner $\left( {1 \times 1} \right)$. So, we can find this for any two consecutive rows and then directly multiply that by the number of pairs of consecutive rows in the chess board to get the required answer. This will be the easiest and efficient way to find the solution of the problem.