Question

The number of ways in which 6 red roses and 3 white roses(all rose different) can form garland that all the white come together is

Answer 1

Hint: First of all, assume all three white roses as a single unit. Now, we have 7 items for the rearrangement in the circular garland. We know the formula for the number of ways of rearrangement for circular permutation for n items, $\dfrac{\left( n-1 \right)!}{2}$ . Using the formula, calculate the number of ways of the rearrangement. Now, we have to rearrange 3 white roses too. The rearrangement in 3 white roses is linear and for the number of ways of linear rearrangement of n items we have the formula, $n!$ . Now, solve it further and calculate the number of ways in which 6 red roses and 3 white roses can be rearranged.

Complete step-by-step answer:
According to the question, it is given that we have some red roses and some white roses and using these roses we have to form a garland. The number of red roses is 6 and the number of white roses is 3.
The total number of red roses = 6 ……………….(1)
The total number of white roses = 3 ………………………(2)
Assume the red roses as ${{R}_{1}},{{R}_{2}},{{R}_{3}},{{R}_{4}},{{R}_{5}},\text{and }{{R}_{6}}$ and white roses as ${{W}_{1}},{{W}_{2}},\text{and }{{W}_{3}}$ .
We have to form a garland in which all the white rose come together. Let us visualize with a diagram,

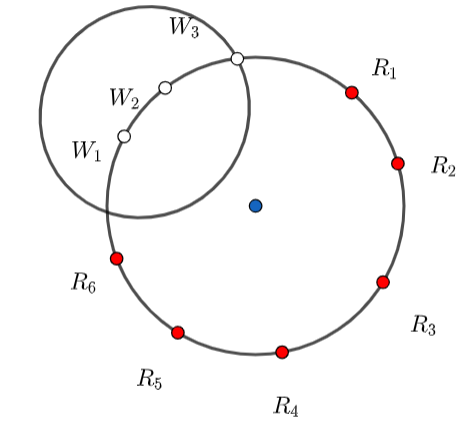
${{R}_{1}},{{R}_{2}},{{R}_{3}},{{R}_{4}},{{R}_{5}},{{R}_{6}},\left[ {{W}_{1}},{{W}_{2}},{{W}_{3}} \right]$
We can assume all three white as a single unit because we have to keep all three white roses together at a place.
So, the number of items for the rearrangement in the garland = 6+1 items = 7 items …………..(3)
We know the formula of the number of ways of rearrangement for circular permutation for n items, $\dfrac{\left( n-1 \right)!}{2}$ …………………(4)
From equation (3), we have the number of items for the rearrangement.
Putting n= 7 in equation (4), we get
$\dfrac{\left( 7-1 \right)!}{2}=\dfrac{6!}{2}$ …………………………(5)
We know the formula that the number of ways for the linear rearrangement of n items is $n!$ …………….(6)
Since we have assumed all the white roses as a single unit but there is also possibility of rearrangement for the white roses as well. The white roses can do rearrangement inside that single unit as shown in figure.
From equation (2), we have the number of white roses.
Using equation (2) and equation (6), we get
The number of ways of rearrangement of 3 white roses = $3!$ ……………………..(7)
Now, from equation (5) and equation (7), we have,
The total possible number of ways = $\dfrac{6!}{2}\times 3!=\dfrac{6\times 5\times 4\times 3\times 2\times 1}{2}\times 3\times 2\times 1=2160$ .
Hence, the total number of ways in which 6 red roses and 3 white roses can form garland that all the white come together 2160.

Note: In this question, one can think to use the formula of the number of ways of rearrangement for circular permutation for 3 white roses because white roses are also a part of the circular permutation. But this is wrong. The white roses are definitely a part of the circular garland but its rearrangement is linear not circular. So, here we have to use the formula of the number of ways for the linear rearrangement.