Solveeit Logo
Login

Question

Question: The number of ways in which 5 boys and 4 girls sit around a circular table so that no two girls sit ...

The number of ways in which 5 boys and 4 girls sit around a circular table so that no two girls sit together is:
(A). 5!4!
(B). 5!3!
(C). 5!
(D). 4!

Explanation

Solution

Hint: In this question it is given that we have to find the number of ways in which 5 boys and 4 girls sit around a circular table so that no two girls sit together. So to find the solution we have to know that the girls have to sit in alternate positions, i.e, there should be one boy in between the girls. So for this we need to know that if there are n number of people sitting on a round table then they can sit (n-1)! different ways. Also we need to know permutation formula which says, if there are n number of quantity and if you want to chose r number of quantity at a time, then we can select in nCr{}^{n}C_{r}, where nPr{}^{n}P_{r} can be written as, nCr=n!(n−r)!{}^{n}C_{r}=\dfrac{n!}{\left( n-r\right) !}

Complete step-by-step solution:
First let us seat the 5 boys in the round table, so in a round table they can seat in (5-1)! =4! Ways.
So the positions of the boys in a round table are shown below.

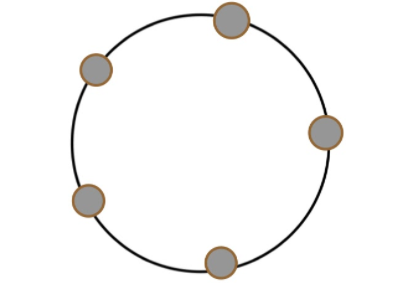
So in between the boys there are 5 positions where the 4 girls can seat, so by using permutation we can say that the 4 girls can seat in 5 different seats in 5P4{}^{5}P_{4} ways.
Since the above two cases are dependent upon each other so we can say that, the total number of ways in which 5 boys and 4 girls sit around a circular table so that no two girls sit together is 4!×5P44!\times {}^{5}P_{4} ways
Since, as we know that, 1! = 1, and n (n - 1)! = n!
Therefore,
Total ways=4!×5P4=4!×5!(5−4)!=4!×5!1!=4!5!4!\times {}^{5}P_{4}=4!\times \dfrac{5!}{\left( 5-4\right) !} =4!\times \dfrac{5!}{1!} =4!5!
Hence the correct option is option A.

Note: While solving this type of problem you might get confused whether to use permutation or combination, so you need to know the difference between them. So the difference between combinations and permutations is ordering. With permutations we care about the order of the elements, whereas with combinations we don't, So that is why in the above we use permutation because here the position of the girls matters.