Question
Question: The number of values of x lying in $[-\pi, \pi]$ and satisfying $2\sin^2 \theta = \cos 2\theta$ and ...
The number of values of x lying in [−π,π] and satisfying 2sin2θ=cos2θ and sin2θ+2cos2θ−cosθ−1=0 is
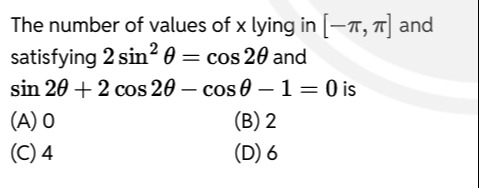
0
2
4
6
2
Solution
Assuming the variable θ in the question is a typo and should be x:
The first equation is 2sin2x=cos2x. Using the identity cos2x=1−2sin2x, we get: 2sin2x=1−2sin2x 4sin2x=1 sin2x=41 sinx=±21
For x∈[−π,π], the solutions are x∈{6π,65π,−6π,−65π}.
For these values, cos2x=1−2sin2x=1−2(41)=21.
The second equation is sin2x+2cos2x−cosx−1=0. Substituting cos2x=21: sin2x+2(21)−cosx−1=0 sin2x+1−cosx−1=0 sin2x−cosx=0
Using sin2x=2sinxcosx: 2sinxcosx−cosx=0 cosx(2sinx−1)=0
This means cosx=0 or sinx=21.
We need to find the values from {6π,65π,−6π,−65π} that also satisfy cosx=0 or sinx=21.
- For x=6π: sinx=21. This satisfies the condition.
- For x=65π: sinx=21. This satisfies the condition.
- For x=−6π: sinx=−21 and cosx=23. This does not satisfy cosx=0 or sinx=21.
- For x=−65π: sinx=−21 and cosx=−23. This does not satisfy cosx=0 or sinx=21.
Thus, the common solutions are x=6π and x=65π. There are 2 such values.
