Question

The number of turns in the coil of an AC generator is 5000 and the area of the coil is $0.25{m^2}$. The coil is rotated at the rate of 100 cycles /sec in the magnetic field of $0.2\dfrac{W}{{{m^2}}}$. Then the peak value will be:
A. 786 kV
B. 440 kV
C. 220 kV
D. 157 kV

Answer 1

In electromagnetic induction when a conductor is moving with certain velocity in the presence of magnetic field then voltage will be generated across the conductor and this is called the induced emf. This happens due to change in the flux which is associated with that conductor. This problem is related to the induced emf.

Formula used:
$\phi = B.A$
\eqalign{ & \phi = BA\cos (\theta ) \cr & \phi = BA\cos (\omega t) \cr}

Complete answer:
Generator is the device which produces the emf due to the magnetic field. It contains a coil. Now if that coil is at rest in the magnetic field then emf is not produced. In order to produce the emf there are two ways. That coil must be in the time varying magnetic field or the coil must be in motion in the magnetic field. This is because emf is generated only if the magnetic flux associated with the coil is varying. Magnetic flux is given as $\phi = B.A$. Where $\phi$ is the flux and B is the magnetic field intensity and A is the area of the coil.
So flux is the dot product of the magnetic field and the area of the coil. If the magnetic field is time varying then if we differentiate flux with time, we get the value of emf. if the area exposed to the magnetic field is varying then if we differentiate the flux we get emf. Another case is if the cosine function in the dot product is time varying then we get emf. In this question we get emf due to this condition only.
Let $\theta$ be the angle between the area vector and the magnetic field vector. It is represented in the diagram below.

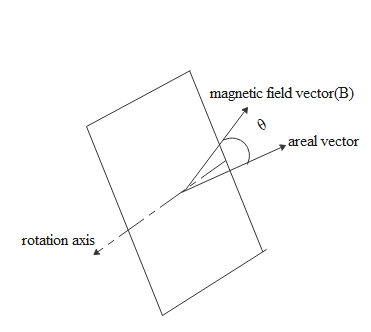
The flux will be
$\phi = BA\cos (\theta )$
Since it will be rotating with time with angular velocity omega we can write it as
$\phi = BA\cos (\omega t)$
\eqalign{ & \Rightarrow \left| {emf} \right| = \dfrac{{d(BA\cos (\omega t))}}{{dt}} \cr & \Rightarrow \left| {emf} \right| = BA\omega \cos (\omega t) \cr & \Rightarrow \left| {emf} \right| = B(Na)(2\pi f)\cos (\omega t) \cr & \Rightarrow \left| {em{f_{maximum}}} \right| = B(Na)(2\pi f) \cr}
Where N is the number of coils and ‘a’ is the area of each coil and ‘f’ is the frequency of rotation.
$\left| {em{f_{maximum}}} \right| = B(Na)(2\pi f)$
\eqalign{ & \Rightarrow \left| {em{f_{maximum}}} \right| = 0.2(5000 \times 0.25)(2\pi \times 100) \cr & \Rightarrow \left| {em{f_{maximum}}} \right| = 157079volts \cr & \Rightarrow \left| {em{f_{maximum}}} \right| \approx 157kilovolts \cr}

Hence option D will be the answer.

Note:
The reason why we use the modulus symbol for the emf is the generated emf will be in such a way that it will oppose the change in the flux. If the flux is increasing the emf generated and hence current is generated in the coil in such a way that the magnetic field due to induced current opposes the flux variation.