Question

The number of solutions of the equation ${{x}^{3}}+{{x}^{2}}+4x+2\sin x=0\text{ in 0}\le \text{x}\le \text{2x}$ is
A. Zero
B. One
C. Two
D. Four

Answer 1

Hint : As the question has algebra and trigonometric combination it is hard to find roots. So, try to separate them and draw graphs of trigonometric and algebraic equations. By this you can get the number of solutions as intersection points.

Complete step by step solution :
Given equation in the question is written in the form as:
${{x}^{3}}+{{x}^{2}}+4x+2\sin x=0\text{ }$
By subtracting 2sinx on both sides of equation, we get it as:
${{x}^{3}}+{{x}^{2}}+4x=-2\sin x$
Let us assume h(x) is a function given by ${{x}^{3}}+{{x}^{2}}+4x$
Let us assume g(x) is a function given by -2sinx
Differentiation of h(x) : $h(x)={{x}^{3}}+{{x}^{2}}+4x$
We know differentiation properties from which we can say:
$\dfrac{d}{dx}{{x}^{n}}={{x}^{n-1}}$
By differentiating on both sides for h(x) equation, we get it as:
$\dfrac{d}{dx}h\left( x \right)=\dfrac{d}{dx}\left( {{x}^{3}}+{{x}^{2}}+4x \right)$
By substituting the differentiation formula, we get it as:
${{h}^{1}}\left( x \right)=3{{x}^{2}}+2x+4$
Now we will find discriminant of this ${{h}^{1}}\left( x \right)$ we get
$D\text{ of a}{{\text{x}}^{\text{2}}}\text{+bx+c=0 is given by }{{\text{b}}^{\text{2}}}\text{-4ac}$
$D\text{ of }{{h}^{1}}\left( x \right)\Rightarrow a=3,b=2,c=4.$
By substituting in formula, we get:
$D\text{ of }{{h}^{1}}\left( x \right)=4-4.4.3$
By simplifying the above equation, we get the D values as:
$D\text{ of }{{h}^{1}}\left( x \right)=4-48$
By simplifying the above equation, we get the value of D as:
$D\text{ of }{{h}^{1}}\left( x \right)=-44$
As we can see, we say the value of D follows inequality: $\text{D}<0$
Whenever we get determinant always negative for ${{f}^{1}}\left( x \right)$ the $\text{f}\left( \text{x} \right)$ is always increasing.
By this statement we can say the graph of ${{x}^{3}}+{{x}^{2}}+4x$ is

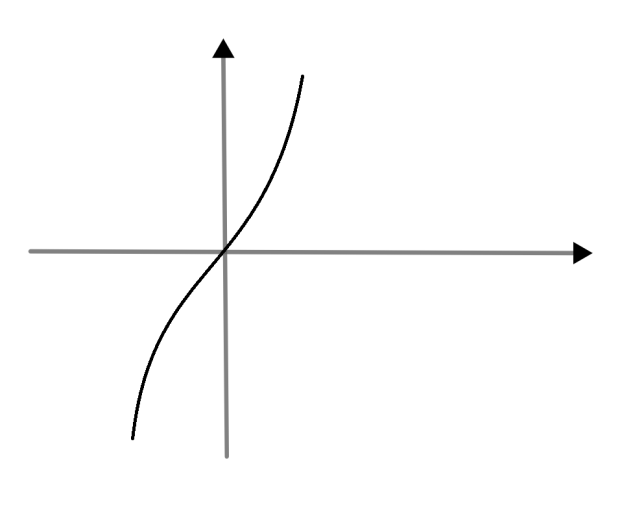
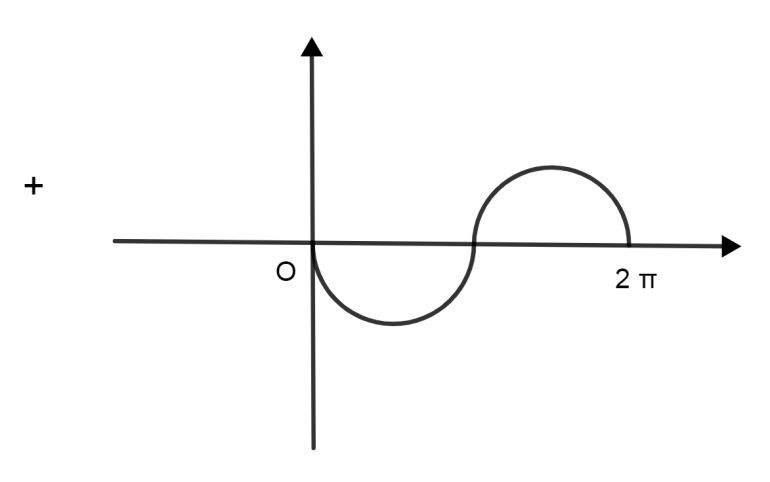
Now we need to plot $-\text{2sinx}$ So, “-“sign depicts that it is a reflection of the x axis to the original graph. 2 depicts that its amplitude increases. By combining above two graphs we get only one solution which is $\text{x}=0$.

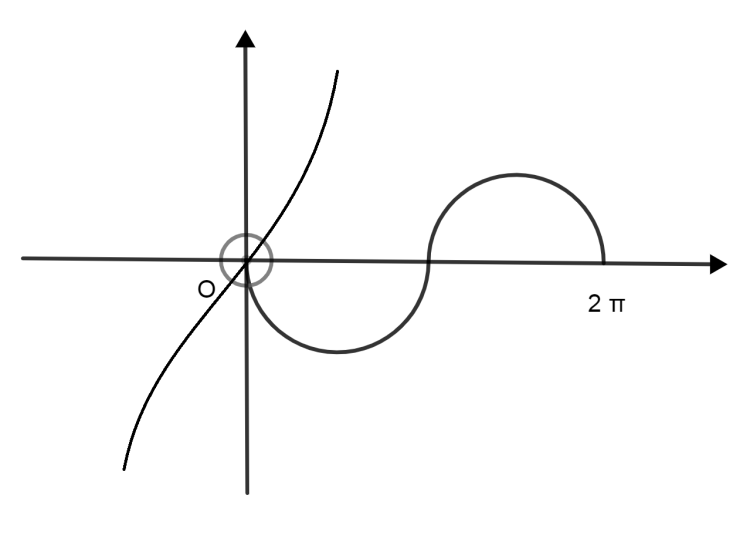
So, the correct answer is “Option B”.

Note : Be careful while differentiating you must check each term because if you miss any term then discriminant value may change. We say upper part of sinx graph does not touch because it a $\pi$ distance from original but ${{\text{x}}^{\text{3}}}$ graph raises to high before that $\pi$ distance so no way that $\text{sinx}$graph touches ${{\text{x}}^{\text{3}}}$ graph other than at point $\text{x}=0$.