Question

The number of solutions of the equation $1 + \sin^4 x = \cos^2 3x, x \in (-\frac{5\pi}{2}, \frac{5\pi}{2})$ is:

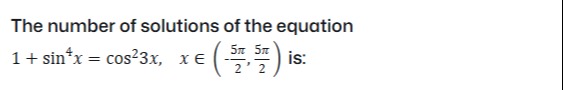
• A. 3
• B. 5
• C. 7
• D. 9

Answer 1

Answer: (B)

5

Answer 2

The equation $1 + \sin^4 x = \cos^2 3x$ implies $1 + \sin^4 x \ge 1$ and $\cos^2 3x \le 1$. For equality, both sides must equal 1. This leads to $\sin^4 x = 0 \implies \sin x = 0$, and $\cos^2 3x = 1$. The condition $\sin x = 0$ gives $x = n\pi$. These solutions always satisfy $\cos^2 3x = 1$. We count the number of solutions $x=n\pi$ in $(-\frac{5\pi}{2}, \frac{5\pi}{2})$, which are for $n \in \{-2, -1, 0, 1, 2\}$. Thus, there are 5 solutions.