Question

The number of solutions of equation

$\begin{vmatrix} 1 & 1 & 1 \\ 1 & 1 + sin\theta & 1 \\ 1 & 1 & 1 + cot\theta \end{vmatrix}=0$ in $\theta \in [0, 2\pi]$ is equal to

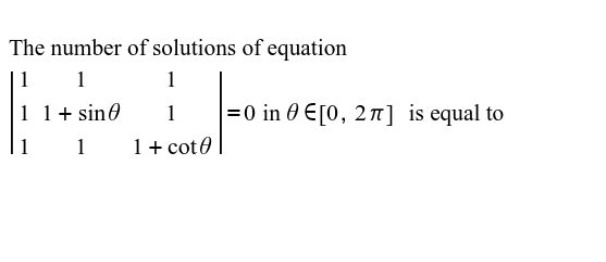
Answer 1

2

Answer 2

We start with the determinant

$$\begin{vmatrix} 1 & 1 & 1 \\ 1 & 1+\sin\theta & 1 \\ 1 & 1 & 1+\cot\theta \end{vmatrix}=0.$$

Subtract the first row from the second and third rows:

$$R_2 \to R_2-R_1,\quad R_3 \to R_3-R_1.$$

This gives

$$\begin{vmatrix} 1 & 1 & 1 \\ 0 & \sin\theta & 0 \\ 0 & 0 & \cot\theta \end{vmatrix} = 1\cdot (\sin\theta \cdot \cot\theta) = \sin\theta\cot\theta.$$

Since $\cot\theta=\frac{\cos\theta}{\sin\theta}$ (provided $\sin\theta\ne0$), we have

$$\sin\theta\cot\theta=\cos\theta.$$

So the equation becomes

$$\cos\theta=0.$$

Within $\theta\in[0,2\pi]$, the solutions are:

$$\theta=\frac{\pi}{2}\quad \text{and}\quad \theta=\frac{3\pi}{2}.$$

Note: The values where $\sin\theta=0$ are not allowed since $\cot\theta$ is undefined there.

Thus, there are 2 solutions.