Question
Question: The number of real roots of the equation $\frac{4x}{x^2+x+3} + \frac{5x}{x^2-5x+3} = \frac{-3}{2}$ i...
The number of real roots of the equation x2+x+34x+x2−5x+35x=2−3 is equal to
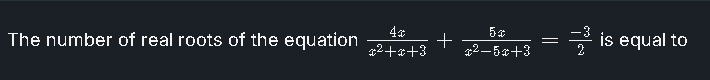
2
Solution
The given equation is: x2+x+34x+x2−5x+35x=2−3
Step 1: Check for x=0.
If x=0, the equation becomes 30+30=0. The right-hand side is 2−3. Since 0=2−3, x=0 is not a root of the equation. This means we can safely divide by x without losing any solutions.
Step 2: Divide numerator and denominator by x.
Since x=0, we can divide the numerator and denominator of each term on the left-hand side by x: xx2+x+3x4x+xx2−5x+3x5x=2−3 x+1+x34+x−5+x35=2−3
Step 3: Introduce a substitution.
Let y=x+x3. Substituting this into the equation: y+14+y−55=2−3
Step 4: Solve the equation for y.
Combine the fractions on the left-hand side: (y+1)(y−5)4(y−5)+5(y+1)=2−3 y2−5y+y−54y−20+5y+5=2−3 y2−4y−59y−15=2−3
Cross-multiply: 2(9y−15)=−3(y2−4y−5) 18y−30=−3y2+12y+15
Move all terms to one side to form a quadratic equation in y: 3y2+18y−12y−30−15=0 3y2+6y−45=0
Divide the entire equation by 3: y2+2y−15=0
Factor the quadratic equation: (y+5)(y−3)=0
This gives two possible values for y: y=−5 or y=3
Step 5: Substitute back and solve for x.
Case 1: y=−5
Substitute y=x+x3: x+x3=−5 Multiply by x (since x=0): x2+3=−5x x2+5x+3=0
This is a quadratic equation in x. Let's find its discriminant, Δ1=b2−4ac: Δ1=(5)2−4(1)(3)=25−12=13 Since Δ1=13>0, this quadratic equation has two distinct real roots.
Case 2: y=3
Substitute y=x+x3: x+x3=3 Multiply by x: x2+3=3x x2−3x+3=0
This is a quadratic equation in x. Let's find its discriminant, Δ2=b2−4ac: Δ2=(−3)2−4(1)(3)=9−12=−3 Since Δ2=−3<0, this quadratic equation has no real roots (it has two complex conjugate roots).
Step 6: Check for domain restrictions.
The original denominators are x2+x+3 and x2−5x+3. For x2+x+3=0, the discriminant is 12−4(1)(3)=1−12=−11<0. So, x2+x+3 is never zero for real x. For x2−5x+3=0, the discriminant is (−5)2−4(1)(3)=25−12=13>0. The roots are x=25±13. The real roots we found from x2+5x+3=0 are x=2−5±13. These are clearly different from 25±13. Also, the values of y we found (y=−5 and y=3) do not make the denominators (y+1) or (y−5) zero in the substituted equation. If y=−1, then x2+x+3=0, which has no real roots. If y=5, then x2−5x+3=0, which has real roots, but our y values are not 5. Thus, the two real roots obtained are valid.
Conclusion:
From Case 1, we found 2 distinct real roots. From Case 2, we found 0 real roots. Therefore, the total number of real roots for the given equation is 2+0=2.
