Question
Question: The number of real numbers x such that $\frac{x}{x+4} = \frac{5[x]-7}{7[x]-5}$ is ______ ([x] denote...
The number of real numbers x such that x+4x=7[x]−55[x]−7 is ______ ([x] denotes greatest integer ≤x).
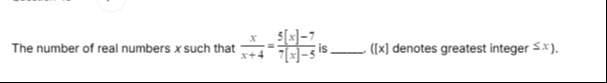
3
Solution
Let k=[x]. Then k is an integer and k≤x<k+1. The given equation is x+4x=7[x]−55[x]−7. Substitute [x]=k: x+4x=7k−55k−7
For the equation to be defined, we must have x+4=0 and 7k−5=0. Since k is an integer, 7k−5=0. Cross-multiply: x(7k−5)=(x+4)(5k−7) 7kx−5x=5kx−7x+20k−28 7kx−5x−5kx+7x=20k−28 2kx+2x=20k−28 2x(k+1)=20k−28 x(k+1)=10k−14
Case 1: k+1=0, i.e., k=−1. In this case, we can solve for x: x=k+110k−14
We use the condition [x]=k, which means k≤x<k+1. Substitute the expression for x: k≤k+110k−14<k+1
We split this into two inequalities:
- k≤k+110k−14
- k+110k−14<k+1
To solve these inequalities, we consider the sign of k+1.
Subcase 1.1: k+1>0, i.e., k>−1. Since k is an integer, k≥0.
-
k(k+1)≤10k−14 k2+k≤10k−14 k2−9k+14≤0 The roots of k2−9k+14=0 are k=2 and k=7. The inequality holds for 2≤k≤7. Since k≥0, the integer values satisfying this are k∈{2,3,4,5,6,7}.
-
k+110k−14<k+1 10k−14<(k+1)2 10k−14<k2+2k+1 0<k2−8k+15 The roots of k2−8k+15=0 are k=3 and k=5. The inequality holds for k<3 or k>5. Since k≥0, the integer values satisfying this are k∈{0,1,2,6,7,8,...}.
For k≥0, we need to find integers k that satisfy both 2≤k≤7 and (k<3 or k>5). The integers satisfying both conditions are k∈{2,6,7}. Let's check the value of x=k+110k−14 for these values of k: If k=2, x=2+110(2)−14=36=2. [x]=[2]=2, which matches k=2. x=2=−4. This is a solution. If k=6, x=6+110(6)−14=746. [x]=[746]=[6+74]=6, which matches k=6. x=46/7=−4. This is a solution. If k=7, x=7+110(7)−14=856=7. [x]=[7]=7, which matches k=7. x=7=−4. This is a solution.
Subcase 1.2: k+1<0, i.e., k<−1. Since k is an integer, k≤−2. When multiplying or dividing by k+1, we reverse the inequality sign.
-
k≤k+110k−14 k(k+1)≥10k−14 k2−9k+14≥0 This holds for k≤2 or k≥7. Since k≤−2, the integers satisfying this are k∈{...,−4,−3,−2}.
-
k+110k−14<k+1 10k−14>(k+1)2 10k−14>k2+2k+1 0>k2−8k+15 This holds for 3<k<5. There are no integers k≤−2 that satisfy 3<k<5. So, there are no solutions in this subcase.
Case 2: k+1=0, i.e., k=−1. The equation x(k+1)=10k−14 becomes x(0)=10(−1)−14, which is 0=−24. This is a contradiction, so there are no solutions when k=−1.
Combining all cases, the possible integer values for [x] are k=2,6,7. For each of these values of k, we found a corresponding value of x: If k=2, x=2. [2]=2. Valid. If k=6, x=46/7. [46/7]=6. Valid. If k=7, x=7. [7]=7. Valid.
We also need to check the original constraint x=−4. The solutions are x=2,x=46/7,x=7. None of these are equal to −4.
Thus, there are exactly 3 real numbers x that satisfy the given equation.
