Solveeit Logo
Login

Question

Question: The number of points in \(\left( { - \infty ,\infty } \right)\), for which \({x^2} - x\sin x - \cos ...

The number of points in (−∞,∞)\left( { - \infty ,\infty } \right), for which x2−xsin⁡x−cos⁡x=0{x^2} - x\sin x - \cos x = 0, is
(A). 6
(B). 4
(C). 2
(D). 0

Explanation

Solution

Before attempting this question, one should have prior knowledge about the concept of increasing and decreasing functions and also remember to differentiate the given function and substitute x = 0, use this information to approach the solution of the problem.

Complete step-by-step answer :
According to the given information we have a function f(x)=x2−xsin⁡x−cos⁡xf\left( x \right) = {x^2} - x\sin x - \cos x
For x = 0
f(0)=(0)2−(0)sin⁡(0)−cos⁡(0)f\left( 0 \right) = {\left( 0 \right)^2} - \left( 0 \right)\sin \left( 0 \right) - \cos \left( 0 \right)
As we know that sin⁡(0)=0\sin \left( 0 \right) = 0and cos⁡(0)=1\cos \left( 0 \right) = 1
Therefore, f(0)=−1f\left( 0 \right) = - 1
Since, the given function which belong to even order and also the trigonometric functions also related
Therefore, for x tends to (−∞,∞)\left( { - \infty ,\infty } \right)value of f(x)f\left( x \right)will be unbounded to infinity
Now, differentiating the given function with respect to x
d(f(x))dx=ddx(x2)−ddx(xsin⁡x)−ddx(cos⁡x)\dfrac{{d\left( {f\left( x \right)} \right)}}{{dx}} = \dfrac{d}{{dx}}\left( {{x^2}} \right) - \dfrac{d}{{dx}}\left( {x\sin x} \right) - \dfrac{d}{{dx}}\left( {\cos x} \right)
As we know that ddx(xn)=nxn−1\dfrac{d}{{dx}}\left( {{x^n}} \right) = n{x^{n - 1}}, by the product rule i.e. ddx(fg)=fddx(g)+gddx(f)\dfrac{d}{{dx}}\left( {fg} \right) = f\dfrac{d}{{dx}}\left( g \right) + g\dfrac{d}{{dx}}\left( f \right)and ddx(cos⁡x)=−sin⁡x\dfrac{d}{{dx}}\left( {\cos x} \right) = - \sin x
Therefore, f′(x)=2x2−1−(xddxsin⁡x+sin⁡xddxx)+sin⁡xf'\left( x \right) = 2{x^{2 - 1}} - \left( {x\dfrac{d}{{dx}}\sin x + \sin x\dfrac{d}{{dx}}x} \right) + \sin x
As we know that ddx(sin⁡x)=cos⁡x\dfrac{d}{{dx}}\left( {\sin x} \right) = \cos x and ddx(xn)=nxn−1\dfrac{d}{{dx}}\left( {{x^n}} \right) = n{x^{n - 1}}
So, f′(x)=2x−(xcos⁡x+sin⁡x)+sin⁡xf'\left( x \right) = 2x - \left( {x\cos x + \sin x} \right) + \sin x
⇒\Rightarrow f′(x)=2x−xcos⁡x−sin⁡x+sin⁡xf'\left( x \right) = 2x - x\cos x - \sin x + \sin x
⇒\Rightarrow f′(x)=2x−xcos⁡xf'\left( x \right) = 2x - x\cos x
For f′(x)=0f'\left( x \right) = 0
2x−xcos⁡x=02x - x\cos x = 0
⇒\Rightarrow x(2−cos⁡x)=0x\left( {2 - \cos x} \right) = 0
Since, maximum value of cos x = 1
Therefore, only when x = 0 f′(x)=0f'\left( x \right) = 0
So, we can say that f′(x)f'\left( x \right)> 0 when x > 0 and < 0 and x < 0
By the above statement we can say that for x < 0 the function is decreasing whereas for x > 0 function is increasing but at x = 0 value of f(0)=−1f\left( 0 \right) = - 1
Therefore, the curve of the function will intersect the x axis two times
So, the graph of the given function will be

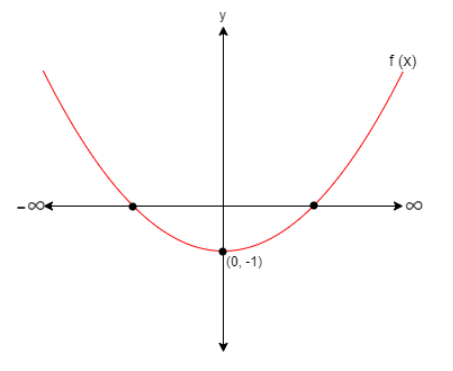
By the above graph we can say that the given function will have 2 numbers of points.
Hence, option C is the correct option.

Note : In the above solution we used the term “function” which can be explained as relation between the provided inputs and the outputs of the given inputs such that each input is directly related to the one output. The representation of a function is given by supposing if there is a function “f” that belongs from X to Y then the function is represented by f:X→Yf:X \to Y examples of function are one-one functions, onto functions, bijective functions, trigonometric function, binary function, etc.