Question

The number of points, having both co-ordinates as integers that lie in the interior of the triangles with vertices (0, 0), (0, 41) and (41, 0) is,
A. 901
B. 861
C. 820
D. 780

Answer 1

Hint:We will be using the concepts of coordinate geometry to solve the problem. We will write inequalities which satisfy the problem and then solve it using analytical skills. We will also use the concepts of arithmetic progression to find the final answer.

Complete step-by-step answer:

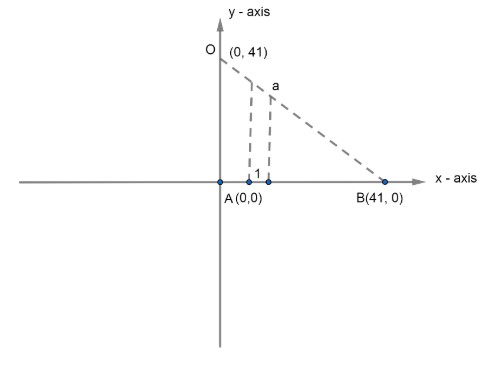
Now, we know that the equation of line in intercept form is $\dfrac{x}{a}+\dfrac{y}{b}=1$. So, equation of OB is,
$\begin{aligned} & \dfrac{x}{41}+\dfrac{y}{41}=1 \\\ & x+y=41 \\\ \end{aligned}$
Now, we have to consider only integer coordinates and that too which is in the interior of triangles. So, all the points must satisfy,

& x+y<41........\left( 1 \right) \\\ & x>0..........\left( 2 \right) \\\ & y>0...........\left( 3 \right) \\\ \end{aligned}$$ Now, if we take x = 1. So, from (2) we have, $\begin{aligned} & 1+y<41 \\\ & y<40 \\\ \end{aligned}$ Also, $y>0$. So, we have 39 points corresponding to x = 1, which satisfy all the three conditions. Now, for x = 2 we have, $\begin{aligned} & 2+y<41 \\\ & y<39 \\\ \end{aligned}$ Also, we have $y>0$. So, we have 38 points corresponding to x = 2. Now, similarly for x = 3, 4 ……..40. We have 37, 36…………..0. So, the number of total points are, $39+38+37+36+......+1$ Now, this forms an A.P with first term a and common difference 1. So, we know that the sum of an A.P is, $s=\dfrac{n}{2}\left( a+l \right)$ Where a is first term and $l$is last term and n is the number of terms. So, we have, $\begin{aligned} & s=\dfrac{39}{2}\left( 39+1 \right) \\\ & =\dfrac{39\left( 40 \right)}{2} \\\ & =39\times 20 \\\ & =780 \\\ \end{aligned}$ Hence, the correct option is (D). Note: To solve these types of questions it is important to draw a graph showing the situation clearly. Also, note how we have generalized the result after finding the number of points for $x=1\ , \ x=2$ and so on.Students have to remember the formula of sum of n terms in an A.P to solve these types of questions.