Question

The number of feet of normal from the point $(7,{\text{ }} - 4)\;$ to the circle ${x^2} + {y^2} = 5$ is
A. 1
B. 2
C. 3
D. 4

Answer 1

First we have to check if the point $(7,{\text{ }} - 4)\;$ lies within the circle ${x^2} + {y^2} = 5$ or outside. Note that, normal drawn from an external point passes through the centre of the circle and hence, intersects the circle at two points.

Complete step by step answer:

__
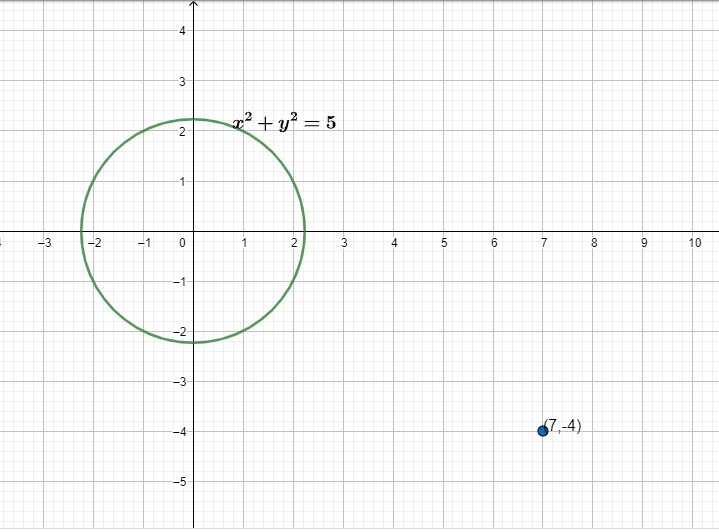
First we have to check if the point $(7,{\text{ }} - 4)\;$ lies within the circle ${x^2} + {y^2} = 5$ or outside.
For this we substitute $x = 7$ and $y = - 4$ in ${x^2} + {y^2}$ . This gives ${\left( 7 \right)^2} + {\left( { - 4} \right)^2} = 49 + 16 = 65$
Since 65 is greater than 5, therefore the point lies outside the circle.
We know that normal drawn from an external point passes through the centre of the circle and hence, intersects the circle at 2 points.
Since, $(7,{\text{ }} - 4)\;$ is an external point to the circle ${x^2} + {y^2} = 5$ , there will be 2 feet of normal.
Hence, the correct option is (B).

Note: The normal to a curve at a given point is the line perpendicular to the tangent at that point. In other words, the line perpendicular to the tangent (to a curve) and passing through the point of contact, is known as the normal. Also, note that normal drawn from an external point passes through the centre of the circle and hence, intersects the circle at two points.