Solveeit Logo
Login

Question

Question: The number of elements in the range of $f(x) = \left[\frac{x}{10}\right]\left[-\frac{10}{x}\right]$,...

The number of elements in the range of f(x)=[x10][−10x]f(x) = \left[\frac{x}{10}\right]\left[-\frac{10}{x}\right], x∈(0,50)x \in (0, 50) are (where [] denotes the greatest integer function)

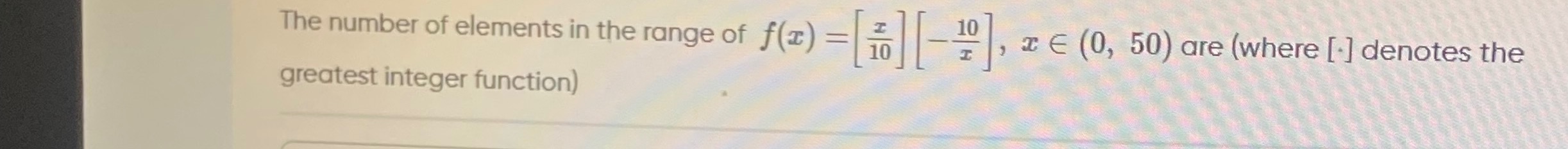
Answer

5

Explanation

Solution

For x∈(0,50)x \in (0,50), we break the domain into segments where the floor function values are constant:

  1. When 0<x<100 < x < 10:

    [x10]=0(since 0<x10<1)\left[\frac{x}{10}\right] = 0 \quad\text{(since } 0 < \frac{x}{10} < 1\text{)}

    Hence, f(x)=0×[−10x]=0f(x) = 0 \times \left[-\frac{10}{x}\right] = 0.

  2. When 10≤x<2010 \le x < 20:

    [x10]=1and[−10x]=−1(because −10x∈[−1,−0.5))\left[\frac{x}{10}\right] = 1 \quad\text{and} \quad \left[-\frac{10}{x}\right] = -1 \quad\text{(because } -\frac{10}{x} \in [-1, -0.5)\text{)}

    Thus, f(x)=1×(−1)=−1f(x) = 1 \times (-1) = -1.

  3. When 20≤x<3020 \le x < 30:

    [x10]=2,[−10x]=−1(since −10x∈[−0.5,−0.333…))\left[\frac{x}{10}\right] = 2,\quad \left[-\frac{10}{x}\right] = -1 \quad\text{(since } -\frac{10}{x} \in [-0.5, -0.333\ldots)\text{)}

    So, f(x)=2×(−1)=−2f(x) = 2 \times (-1) = -2.

  4. When 30≤x<4030 \le x < 40:

    [x10]=3,[−10x]=−1\left[\frac{x}{10}\right] = 3,\quad \left[-\frac{10}{x}\right] = -1

    Hence, f(x)=3×(−1)=−3f(x) = 3 \times (-1) = -3.

  5. When 40≤x<5040 \le x < 50:

    [x10]=4,[−10x]=−1\left[\frac{x}{10}\right] = 4,\quad \left[-\frac{10}{x}\right] = -1

    So, f(x)=4×(−1)=−4f(x) = 4 \times (-1) = -4.

Distinct values in the range: {0,−1,−2,−3,−4}\{0, -1, -2, -3, -4\}

Thus, the number of elements in the range is 5.