Question

The number of electric field lines leaving the positive charge 0.5C charge placed in the medium of dielectric constant $K=10$ is –

& \text{A) 5}\text{.65}\times \text{1}{{\text{0}}^{9}} \\\ & \text{B) 1}\text{.13}\times \text{1}{{\text{0}}^{11}} \\\ & \text{C) 9}\times \text{1}{{\text{0}}^{9}} \\\ & \text{D) 8}\text{.85}\times \text{1}{{\text{0}}^{-12}} \\\ \end{aligned}$$

Answer 1

We need to find the relation between the electric field due to a charge, the number of electric field lines, and the dielectric constant in the system of a charge. We can relate this using the formula for electric field strength from Coulomb's law.

Complete step-by-step solution:
The number of electric field lines emerging from a charge is the electric flux of the system. It is defined as the number of electric field lines produced by a charge enclosed in a given area surrounded by the charge at a distance ‘r’ from the charge.
We know that the electric field strength is given from Coulomb's law as the force experienced per unit charge by a charge due to another charge at a distance ‘r’. It is given as – $E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{r}^{2}}}$
Now, we can find the number of field lines due to the charge ‘q’ in an area enclosed within ‘r’ units from the charge.

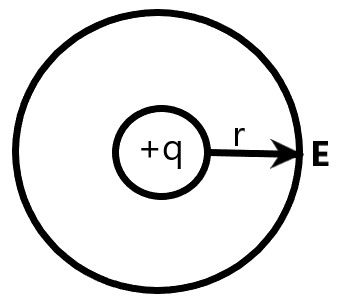
The electric flux is given as –
$\phi =E.A$
The area of the surface enclosed which is equidistant from the charge ‘q’ is a sphere whose surface area will be –
$A=4\pi {{r}^{2}}$
Now, we can find the number of field lines or electric flux for a charge 0.5C placed in dielectric medium with $K=10$ is given as –
$E=\dfrac{1}{4\pi \varepsilon }\dfrac{q}{{{r}^{2}}}$
$\Rightarrow E=\dfrac{k}{K}\dfrac{q}{{{r}^{2}}}$
$\text{where,}$
$k=\dfrac{1}{4\pi {{\varepsilon }_{0}}}$
$\text{and,}$
$\text{K=}\dfrac{\varepsilon }{{{\varepsilon }_{0}}}$
$\text{Also,}$
$A=4\pi {{r}^{2}}$
$\text{Now,}$
$\phi =E.A$
$\Rightarrow \phi =\dfrac{k}{K}\dfrac{q}{{{r}^{2}}}4\pi {{r}^{2}}$
$\Rightarrow \phi =\dfrac{9\times {{10}^{9}}\times 0.5\times 4\pi }{10}$
$\therefore \phi =5.65\times {{10}^{9}}$
The electric flux or the number of field lines passing through the surface of the sphere at a distance ‘r’ from the charge is $\phi =5.65\times {{10}^{9}}$.
The correct answer is option A.

Note: The concept of electric flux density is more popularly used than the number of field lines or the electric flux. It is the concentration of field lines at distance from the charge. For a parallel field, the electric flux is independent of the distance from the source.