Question

The number of corner of O-atoms shared per tetrahedron in 2D- silicate is:
[A] 3
[B] 4
[C] 2
[D] 5

Answer 1

Silicates contain a silicon atom that is covalently bonded to four oxygen atoms. 2D silicates are also known as sheet silicates. They form a sheet like structure where the structure is formed by sharing of oxygen atoms.

Complete step by step answer:
Before discussing the answer, we will discuss what silicates are and their varieties.
We know that all silicates contain tetrahedral $Si{{O}_{4}}^{4-}$ anions. Si i.e. silicon in the silicates are $s{{p}^{3}}$ hybridised with 4 covalent bonds with the 4 negatively charged oxygen atoms. Different structures of silicates are based on the nature of linking between the tetrahedral $Si{{O}_{4}}^{4-}$ ions.
There are ortho silicates in which none of the oxygen atoms are shared, pyro silicates in which one oxygen atom is shared and there are many more such possibilities.
Now let us discuss 2D silicates.
These silicates are also known as sheet silicate or phyllosilicate. In this type of silicates, the $Si{{O}_{4}}^{4-}$ tetrahedron units have all three corners attached to three different $Si{{O}_{4}}^{4-}$ tetrahedron units resulting in a sheet structure.
The simplest sheet silicate is $S{{i}_{2}}{{O}_{5}}^{2-}$. We can draw its structure as-

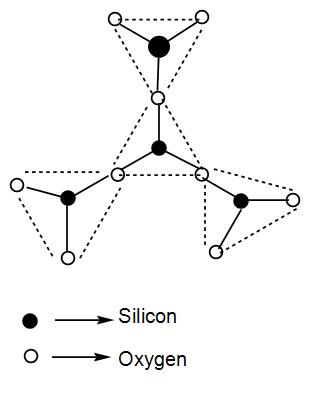
The general formula of phyllo or 2d silicates is ${{(S{{i}_{2}}{{O}_{5}})}_{n}}^{2-}$

Here, all the three oxygen atoms of the tetrahedron are shared with other similar units. In the above diagram we have not drawn the sheet structure but just one unit cell of the complete structure where all the three oxygen atoms will be shared.
We can understand from the above discussion that the number of corners of O-atoms shared per tetrahedron in 2D- silicate is 3.
So, the correct answer is “Option A”.

Note: Example of a sheet silicate is Soapstone. Its formula is $M{{g}_{3}}{{\left( OH \right)}_{2}}S{{i}_{4}}{{O}_{10}}$. Here, cations between the alternate layers leave only Van der Waals forces between corresponding layers making the mineral very soft and slippery.
Special case of sheet silicates is Mica. Here, one silicon atom is replaced by an aluminium atom. Instead of $S{{i}_{4}}{{O}_{10}}$ , we get to see $S{{i}_{3}}Al{{O}_{10}}^{5-}$ . The formula of mica is $KM{{g}_{3}}{{\left( OH \right)}_{2}}S{{i}_{3}}Al{{O}_{10}}$.