Solveeit Logo
Login

Question

Question: The number of common tangents to $x^2+y^2-6x-10y+33=0$ and $x^2+y^2-2y=0$ is _____....

The number of common tangents to x2+y2−6x−10y+33=0x^2+y^2-6x-10y+33=0 and x2+y2−2y=0x^2+y^2-2y=0 is _____.

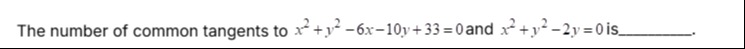
Answer

4

Explanation

Solution

  1. Find centers and radii:

    For the circle

    x2+y2−6x−10y+33=0,x^2 + y^2 - 6x - 10y + 33 = 0,

    complete the square:

    (x2−6x)+(y2−10y)=−33,(x^2 - 6x) + (y^2 - 10y) = -33, (x−3)2−9+(y−5)2−25=−33⇒(x−3)2+(y−5)2=1.(x-3)^2 - 9 + (y-5)^2 - 25 = -33 \quad \Rightarrow \quad (x-3)^2 + (y-5)^2 = 1.

    Thus, center (3,5)(3,5) and radius 11.

    For the circle

    x2+y2−2y=0,x^2 + y^2 - 2y = 0,

    complete the square:

    x2+(y2−2y)=0,x^2 + (y^2 - 2y) = 0, x2+(y−1)2−1=0⇒x2+(y−1)2=1.x^2 + (y-1)^2 - 1 = 0 \quad \Rightarrow \quad x^2 + (y-1)^2 = 1.

    Thus, center (0,1)(0,1) and radius 11.

  2. Distance between centers:

    d=(3−0)2+(5−1)2=9+16=5.d = \sqrt{(3-0)^2 + (5-1)^2} = \sqrt{9 + 16} = 5.

  3. Determining the number of common tangents:

    Since the distance between the centers d=5d = 5 is greater than the sum of the radii 1+1=21+1 = 2, the circles are completely separate (externally disjoint). Hence, there are 4 common tangents.