Question

The number $(2 + \sqrt{3})^6$ of can be expressed in the form $k + \sqrt{k^2 - 1}$ where $k$ is a positive integer, then $k$ = (where [.] denotes greatest integer function)

Answer 1

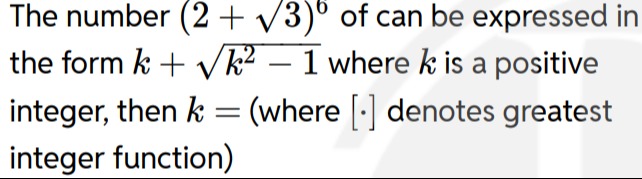
1351

Answer 2

To express $(2 + \sqrt{3})^6$ in the form $k + \sqrt{k^2 - 1}$, we can proceed as follows:

1. Expand using the Binomial Theorem:

   Let $x = (2 + \sqrt{3})^6$. We consider also $y = (2 - \sqrt{3})^6$.

2. Compute $x + y$:

   Using the binomial expansion formula for $(a+b)^n + (a-b)^n = 2[\binom{n}{0}a^n + \binom{n}{2}a^{n-2}b^2 + \binom{n}{4}a^{n-4}b^4 + \dots]$:

   $x + y = (2 + \sqrt{3})^6 + (2 - \sqrt{3})^6 = 2 \left[ \binom{6}{0}2^6 + \binom{6}{2}2^4(\sqrt{3})^2 + \binom{6}{4}2^2(\sqrt{3})^4 + \binom{6}{6}(\sqrt{3})^6 \right]$

   $x + y = 2 \left[ 1 \cdot 64 + 15 \cdot 16 \cdot 3 + 15 \cdot 4 \cdot 9 + 1 \cdot 27 \right] = 2[64 + 720 + 540 + 27] = 2[1351] = 2702$

3. Compute $x - y$:

   Using the binomial expansion formula for $(a+b)^n - (a-b)^n = 2[\binom{n}{1}a^{n-1}b + \binom{n}{3}a^{n-3}b^3 + \binom{n}{5}a^{n-5}b^5 + \dots]$:

   $x - y = (2 + \sqrt{3})^6 - (2 - \sqrt{3})^6 = 2 \left[ \binom{6}{1}2^5\sqrt{3} + \binom{6}{3}2^3(\sqrt{3})^3 + \binom{6}{5}2^1(\sqrt{3})^5 \right]$

   $x - y = 2 \left[ 6 \cdot 32\sqrt{3} + 20 \cdot 8 \cdot 3\sqrt{3} + 6 \cdot 2 \cdot 9\sqrt{3} \right] = 2 \left[ 192\sqrt{3} + 480\sqrt{3} + 108\sqrt{3} \right] = 2[780\sqrt{3}] = 1560\sqrt{3}$

4. Find the expression for $(2 + \sqrt{3})^6$:

   $(2 + \sqrt{3})^6 = \frac{(x+y) + (x-y)}{2} = \frac{2702 + 1560\sqrt{3}}{2} = 1351 + 780\sqrt{3}$

5. Compare with the given form $k + \sqrt{k^2 - 1}$:

   We have $(2 + \sqrt{3})^6 = 1351 + 780\sqrt{3}$. Comparing this with $k + \sqrt{k^2 - 1}$, we can identify $k = 1351$. Now, we need to verify if $780\sqrt{3}$ is indeed equal to $\sqrt{k^2 - 1}$ for $k=1351$.

   Square $780\sqrt{3}$: $(780\sqrt{3})^2 = 780^2 \cdot 3 = 608400 \cdot 3 = 1825200$.

   Calculate $k^2 - 1$ for $k=1351$: $k^2 - 1 = 1351^2 - 1 = (1351-1)(1351+1) = 1350 \cdot 1352 = 1825200$.

   Since $(780\sqrt{3})^2 = 1825200$ and $k^2 - 1 = 1825200$, it confirms that $780\sqrt{3} = \sqrt{k^2 - 1}$ for $k=1351$.

Thus, the value of $k$ is $1351$.