Question
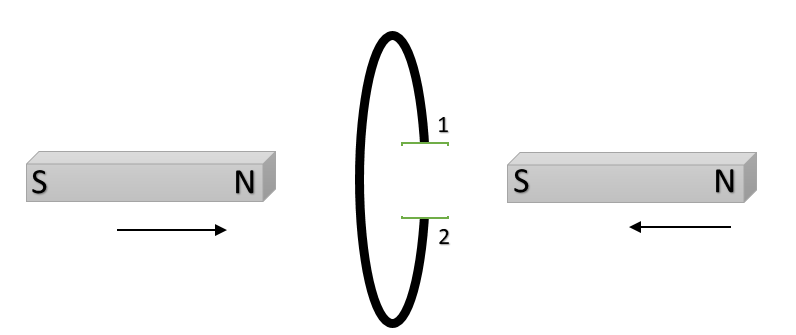
Question: The north and south poles of two identical magnets approach a coil, containing a condenser, with equ...
The north and south poles of two identical magnets approach a coil, containing a condenser, with equal speed from opposite sides. Then
A. Plate 1 will be negative and plate 2 positive
B. Plate 2 will be positive and plate 2 negative
C. Both the plates will be positive
D. Both the plates will be negative.
Solution
These types of problems could be easily solved by applying the basic statement of Lenz law, which states that emf is generated if the magnetic flux linked with a coil changes. The direction of emf is such that it opposes the cause of motion or effect.
Complete answer:
According to Faraday’s law, if there is a change in flux in a coil, it will produce or generate an E.M.F. in the coil. According to Lenz law, the change in magnetic field is opposed in such a manner that the current inside the coil will resist the magnetic field by flowing in a particular direction.
Now, as we know that magnetic field is generated from the north pole of the magnet and enters the south pole of the magnet. Now, as the two magnets approach each other, more and more magnetic lines of flux enter the loop. This means the magnetic field is increasing from left to right.
Now, according to Lenz law, the loop will oppose the cause of this increase in magnetic field. Hence the loop will produce the magnetic field from right to left (in order to oppose).
Now, to produce the magnetic field from right to left, the current must be flowing from ‘2’ to ‘1’. This is because a current carrying wire starts acting as a small bar magnet. Thus, point ‘2’ must be high potential.
So, the correct answer is “Option B”.
Note:
Lenz law is just an extension of Faraday’s law. According to Faraday’s law, the E.M.F. produced inside a coil is has a magnitude equal to the rate of change of magnetic flux i.e. ∣ε∣=dtdϕ. But the direction in which the current will flow (i.e. clockwise or anti-clockwise) is given by Lenz law. Hence the complete law is ε=−dtdϕ.
